Lecture by Prof Imre Leader
This was a lecture given by Prof Imre Leader on many months ago on February 14 2024 (Valentine’s day lol) when he was visiting Singapore. I attended this lecture the day before I flew off to South Africa later during midnight for Exercise Brightfire (XBF). Super glad that I could attend it! Prof Leader is a really an excellent lecturer!
Since I found this lecture so amazing, I would like to record it down in this blog post. Some details might be different from the lecture he gave cause I’m recalling it from 8 months ago…
The theme of this lecture was on catching games. Because this is mathematics, we will assume that all entities can react instantly.
Before attending this lecture, I knew about similar games:
Cat and Mouse Game
There is a cat and mouse with speeds $v_c$ and $v_m$ respectively. The cat wants to eat the mouse and the mouse doesn’t want to get eaten (duh). We will assume that the cat and mouse don’t start on the same point or the mouse will get eaten immediately.
First, we consider when the cat and mouse lives on the border of a $2$-dimensional circle. It is identical to taking the number range $[0,1]$ and gluing $0$ to $1$.
When will the cat eat the mouse? Obviously, it is when $v_c > v_m$. Ok very boring.
Let’s consider that the cat and mouse are instead playing on the graph of $K_4$ with all edges having the same length. If you don’t like graphs, you can think of them as playing on the edges of a regular tetrahedron.
When will the cat eat the mouse now? It is when $v_c > v_m$.
Proof
Suppose that $v_c > v_m$. Now, the strategy for the cat is to first take any path to the initial position of the mouth and then mirror its move. The cat will eventually end up in the end position as the mouse.
Suppose that $v_c \leq v_m$. We can actually reduce this case into the earlier case of a circle. The idea is for the mouse to choose a face of the tetrahedron and declare that he will only stay in that face of the tetrahedron. Then, we embed all other points of the tetrahedron into that face so that the embedding is continuous (no tearing) and it doesn’t give the cat any advantage.
If we use the graph representation of $K_4$, this means the mouse says he will only stay in the subgraph generated by vertices $1,2,3$. Then our embedding is to merge vertices $3$ and $4$. If we use the geometric tetrahedron representation, then we can imagine that we rotate the tetrahedron until two vertices have the same $x$ and $y$ coordinate, then we squish the $z$ coordinate.
Our embedding does not give our cat any advantage over the earlier circle case. So the cat still loses
Ok that was not that interesting as well. What if there were two cats? Well, our poor mouse can lose even if $v_m = \infty$ if he is pincered by the cats. So let’s allow our mouse to choose his position after knowing where the cats will start.
It turns out that if the two cats have speeds $v_{c_1} = \frac{v_m}{2}$ and $v_{c_2} = \epsilon$, it is enough to catch the mouse!
Proof
Let’s ignore cat $c_2$ for now.
First, choose some edge of the tetrahedron $AB$. Cat $c_1$ will say that he will only stay on that edge. We will embed the rest of the tetrahedron onto $AB$. Let $M$ be the midpoint of edge $AB$. Then we will embed edges $AC$ and $AD$ into $AM$, edges $BC$ and $BD$ into $BM$ and $CD$ into $MM$.
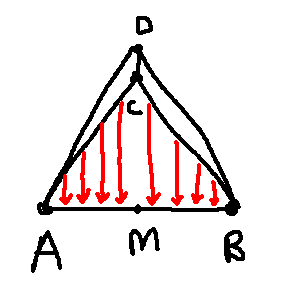
Suppose the mouse and the cat are currently on the same point in the embedding (but not on the tetrahedron or the mouse will die). $AC$ of length $1$ is embedded into $AM$ of length $\frac 12$. So even though the cat has speed $v_{c_1} = \frac {v_m} 2$, the cat can still remain on the same point as the mouse on this embedding. Then, the mouse can never touch the edge $AB$ (including the endpoints).
As for how the cat can force the mouse to be on the same embedded point as him, well the cat just needs to move towards the mouse in this embedding.
Now our cat $c_2$ with speed $v_{c_2} = \epsilon$ comes into play. Currently, the mouse is trapped in the tetrahedron minus the edge $AB$ but notice that this is acyclic! Therefore the cat can always catch the mouse no matter how slow it is moving.
Wolf Game
Now, we will look at a totall different class of games. There is a regular $n$-gon ($n \geq 3$). A man is trapped inside this regular $n$-gon and there are $m$ wolves that want to eat the man. All entities have the same speed here. But they can only stay on the border of the $n$-gon. Also, we will allow the wolves to choose their starting knowing the starting position of the man, because the man can win if we make the starting positions really silly.
Now, $n$ wolves is enough.
Proof
We will ask each wolf to stay on a single side of the $n$-gon such that if the man tries to escape from that side of the $n$-gon, the wolf will stop him from doing so.
The construction is very simple, extend rays from the man that are perpendicular to the side of the $n$-gon. The wolf will follow the projection of this ray on the side of the $n$-gon.
If $n \geq 5$, it is possible that the ray will be projected outside the side of the $n$-gon. But this is fine, the wolf just waits at the end of this side that is closer to the projection.
The diagram below should make it clear.
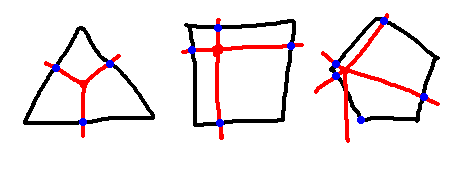
In this strategy, the wolves can obviously keep up with the projection of the man into their respectively sides.
Now, is this optimal? For $n \leq 4$, there is a simple proof for this.
Note that this proofs below are mine. Prof Leader did not go through the proof during this lecture cause he said it was “by geometry or something”.
Proof for $n=3$
Let’s look at the simpler case of $n=3$ and show that the man can escape when there are $2$ wolves.
Let the man first go to the center of the triangle. There are $3$ different points on the border of the triangle that are closest to the man. Call these good points.

If we let the distance between an good point and the center be $1$, then the distance between $2$ adjacent good points travelling through the border can be calculated to be $2\sqrt{3}$. No matter where the wolf is initially on the border, he can only guard at most $1$ good point. Since there are $3$ points and only at most $2$ wolves, the man can escape through the unguarded good point.
Proof for $n=4$
Does the proof for $n=3$ work for $n=4$? No. This is because now a single wolf can guard $2$ of the $4$ good points instead. So our proof technique cannot even prove that we need at least $3$ wolves for $n=4$.
But observe that when a wolf covers $2$ good points, he barely does so.
So instead of having good points be those that are at most $1$ away from the center of the square, the good points are those with distance at most $\sqrt{1+\epsilon^2}$ away. So the sum of distance that the man can escape is now $8 \epsilon$. Then we show that $3$ wolves cannot guard all these points.
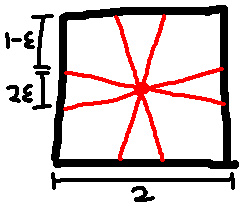
It is easy to see that the maximum distance of good points that a single wolf can cover is $2\sqrt{1+\epsilon^2} - 2(1-\epsilon) = 2 (\sqrt{1+\epsilon^2} - \sqrt{1-2\epsilon+\epsilon^2}) \leq 2 \frac{2\epsilon}{2\sqrt{1-2\epsilon+\epsilon^2}} = \frac{2\epsilon}{1-\epsilon}$, since $\sqrt{x}$ is concave,
Therefore, in the best case, a single wolves can only cover a distance of $\frac{2 \epsilon}{1- \epsilon}$. But it is easy to see that for small enough $\epsilon >0$, we have $8\epsilon > \frac{6 \epsilon}{1-\epsilon}$.
Now, Prof Leader did not touch about the lower bound for $n \geq 5$. Instead he asked us what we thought the optimal answer for a $\infty$-gon (a circle) as.
If I recall correctly, he polled people to ask whether we thought it was $4$, $5$, $6$, $7$, $8$, or more than that. I got trolled and thought it was $6$ for some reason.
Turns out that no finite number of wolves suffices for this case.
Even more crazier, no countably infinite number of wolves suffices….
Proof
This proof is super handwavy.
The high level strategy is that we define a procedure made of a countably infinite number of steps where in the $i$-th step, we guarantee that the man would not get eaten by the $i$-th wolf. And at the end of all those steps, the man would be on the border of the circle and will have therefore escaped.

In the $i$-th step, suppose that we have constrained the man to stay in some sector rooted at point $O$, where $O$ might not be the origin of the circle. We will first move downwards towards point $A$. Now, depending on whether the wolf $w_i$ is on the left or right of us, we will move right or left respectively to point $B$ for example, then we do the $i+1$-th step with our section rooted at point $B$. Then we need to show that no matter what we do in the sector rooted at point $B$, we can ensure that the wolf will not enter the sector rooted at point $B$ as long as don’t spend too long before escaping.
And as an immediate corollary, we get a proof that $\mathbb{R}$ is not countable. Because we could just place one wolf at each real number radian between $0$ and $\tau$ and the man will not be able to escape.
Man and Lion Game
Now, the final game introduced in Prof Leader’s lecture.
There is a man and lion in a roman colosseum (it is a circle, so the man cannot run off into infinity). Both the man and the lion has the same speed. What are the strategies for both players?
Strategy 1
It seems that the man’s strategy should be running around and around the parameter of the circle and the lion’s strategy should be to run in the direction of the man.
This will result in the Lion running in spirals that get arbitrarily to the man, but the Lion will not catch the man using finite time.
Prof Leader didn’t give a proof. But it seems intutively correct to me.
Strategy 2
But actually, the Lion has a better strategy here. He should always stay on the line joining the man and the origin. It is sort like a Bézier curve.
Let us give the circle a radius of $1$ and the man runs at a speed of $1$ for convenience.
Then if we give the lion the polar coordinates $(r,\theta)$, we have that $\frac{d\theta}{dt} = 1$. Now, we want the speed of the Lion to also be $1$. The speed of the Lion is given by $\sqrt{(\frac{dr}{dt})^2 + (r\frac{d\theta}{dt})^2}$. So we have $\frac{dr}{dt} = \sqrt{1 - r^2}$.
So we need to solve $t = \int \frac{1}{\sqrt{1-r^2}} \, dr$, which we know is $t = \arcsin(r)$. OK, so $r(t) = \sin(t)$, very cool!
And then we know that $\theta(t)=t$ also, so we have the polar equation $r(\theta) = \sin(\theta)$. Which we know is a circle!
What a beautiful piece of math! The path the Lion would trace is a semicircle!

I wish I was able to produce a Gif, but I cannot find one.
So, according to Prof Leader, this was the solution for many years. The Lion had a really beautiful strategy to win. But some years later, some Russian mathematician realized that the strategy of the man wasn’t correct.
Strategy 3
Why did we assume that the man should run on the border? Indeed, there is a strategy that the man can follow to never be eaten!
Suppose that the man is on polar coordinate $(r,\theta)$. Consider the line joining the man to the origin. There are 2 cases:
- The lion is on the left side of the line, the man runs perpendicular to the line to the right
- The lion is on the right side of the line, the man runs perpendicular to the line to the left

The man will not get eaten unless he reaches the border. So let us suppose we runs in a straight line for time $t$. What will be his new value of $r$? Using Pythagoras theorem, it is $\sqrt{r^2+t^2}$. So $t^2$ gets added to the squared radius.
Now, you might see where this is going. Let $t_1,t_2,\ldots$ be a sequence of numbers. Where the man will do the above strategy for some time steps where in the $i$-th step, he will run for $t=t_i$.
Using this strategy, the man will use $\sum t_i$ time and will have a final radius of $\sqrt{\sum t_i^2}$.
Now, as long as we can find a sequence $t$ such that $\sum t_i$ converges and $\sum t_i^2$, we are done! The man will stay a finitely large circle for any finite time.
And does such a sequence exist? Yes! $t_i = \frac{1}{i}$ works.
Prof Leader provided the following proofs:
$\sum t_i$ is the harmonic sum problem which we know grow at around $\log n$.
$\begin{align} &\frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \ldots \\ \geq& 1 + \frac{1}{2} + (\frac{1}{4} + \frac{1}{4}) + (\frac{1}{8} +\frac{1}{8} +\frac{1}{8} +\frac{1}{8} ) + \ldots \\ =& 1 + \frac{1}{2} + \frac{1}{2}+ \frac{1}{2} + \ldots = \infty \end{align}$
$\sum t_i^2$ is the Basel problem which we know is $\frac{\pi^2}{6}$, but there is a much simpler proof that it converges. For reference for the answer to Basel problem, I like 3b1b’s video on it.
$\begin{align} &\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \ldots \\ \leq& 1 + \frac{1}{1 \cdot 2} + \frac{1}{2 \cdot 3} +\frac{1}{3 \cdot 4} +\frac{1}{4 \cdot 5} + \ldots \\ =& 1 + (\frac{1}{1}- \frac{1}{2}) + (\frac{1}{2}- \frac{1}{3}) + (\frac{1}{3}- \frac{1}{4}) + (\frac{1}{4}- \frac{1}{5}) + \ldots = 2 \end{align}$
Now, a interesting property of this is that we can make $t_i = \frac{\epsilon}{i}$, so the man can win as long as there is a (possibly small) neighborhood to run in.
Q&A
Someone asked a question about generalizations of the Lion and Man problem, which Prof Leader said that the following was an open problem:
There is a connected lake in the middle of the circle and there are 2 lions. Can the man win? The lake needs to be rectifiable or else it can be a funny spiral and the man can just run into the spiral.
I decided to ask the classic question “why does anyone care about this”?
Surprisingly, Prof Leader had a very good answer to this question. There is a book Differential Games by Isaacs. If you look at an older manuscript, you will see that the work was done under U.S. Air Force and it even states on the summary that “… [the more cogent applications] are largely military such as pursuit, battle, and aiming games”. Why would the U.S. Air Force care about such things? Well, what if we replaced Lion by missile and Man by an aircraft?
This research might give insights into how pilots should fly during dog fighting. Of course, in real life it gets more complicated. Real projectiles has turning radiuses, acceleration times, etc. But it just goes to show how such seemingly “useless” mathematics actually has its uses. This kind of hit me because as I said at the start of the blog, I was flying off to Exercise Brightfire literally the next day to shoot a missile. For the application to hit so close to home on a random mathematics lecture was a really weird feeling.