Meta Hacker Cup 2024
I did not qualify for Round 3 of Meta Hacker Cup this year. Not that salty tbh. I think that I’ve become old and jaded or something. Spending 3 hours from 1-4am coding just doesn’t hit the same as when I was still in highschool.
I placed 32rd on round 1 and 564th on round 2. I had 1 FST on round 1 and 2 FSTs on round 2 (which was the reason I didn’t get to round 3 lol).
1C
Suppose we are of weight $x$ and the minimum weight we have ever been is $x$ also. We want to calculate the expected number of steps until we hit weight $x-1$ for the first time.
My solution was this. With equal chance, we will do $x:=x-1$ and $x:=x+1$.
If we do $x:=x-1$, we will hit weight $x-1$ using $1$ move. Easy.
If we do $x:=x+1$, observe that the expected number of moves to move to $x$ again is when the problem has $L’=L-1$.
Let us define $E(l)$ to be the expected number of steps until we hit weight $x-1$ for the first time when we have $L=l$.
We know that $E(0)=1$ and have the recursive formula $E(l) = \frac{1}{2}((1)+(E(l-1)+E(l)+1)$, which simplifies to $E(l) = E(l-1) + 2$, therefore, we find that $E(l) = 2l+1$.
But there is another technique to solve these sort of markov chain problems. Thank you to MridulAhi for sharing this trick.
Given a markov chain graph (that inlcudes source and sink), we want to find the expected number of times we traverse each edge. We can fill each edge using the following property:
- (1): For all edges with the same outgoing vertex, their expected value is proportional to the probability of leaving through those edges.
- (2): For all vertices (except source and sink), sum of incoming and sum of outgoing must be same.
- (3): If the problem constraints has edges $u$ and $v$ such that for any configuration, $u=v+c$, then obviously we have $E(u)=E(v)+c$.
The proofs of all the 3 statements above are obvious. But they working surprisingly well for many markov chains.
Now, conditions (1) and (2) are already sufficient to solve this problem.
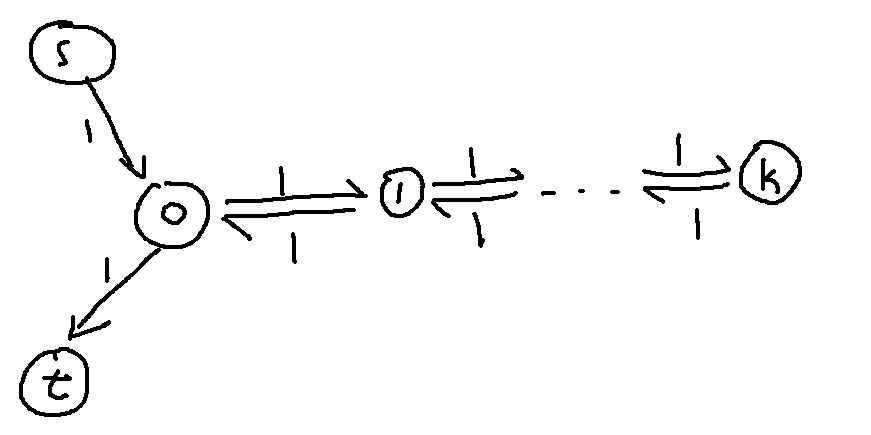
Let $E_{u,v}$ denote the expected number of times we traverse the edge from $u$ to $v$.
From property (1), $E_{0,1} = E_{0,t}=1$. So $E_{0,1}=1$.
From property (2), $E_{0,1}+E_{0,t} = E_{s,0} + E_{1,0}$. So $E_{1,0}=1$. Although property (3) is more obvious here.
Using property (1) and (2) in a similar way, we can observe that $E_{x,x+1}=E_{x+1,x}=1$.
It can even solve CF1823F easily! Let us look at this toy graph.
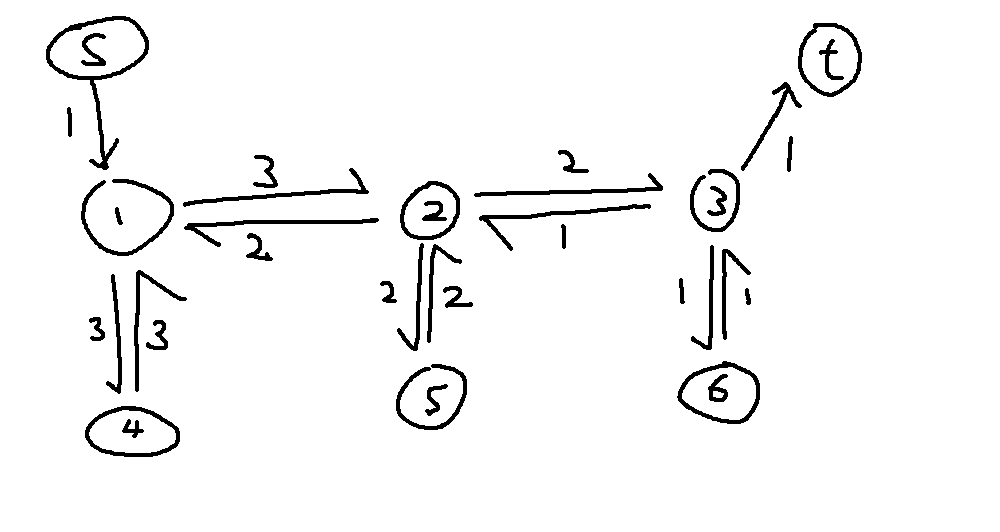
From property (1), we have $E_{3,2}=E_{3,6}=E_{3,t}=1$.
From property (3), we have $E_{2,3}=E_{3,2}+1=2$ and $E_{6,3}=E_{3,6}=1$.
Using property (1) and (3) in a similar way, we can fill the rest of the graph.
Just for fun, we can also do this for the shikanoko markov chain.
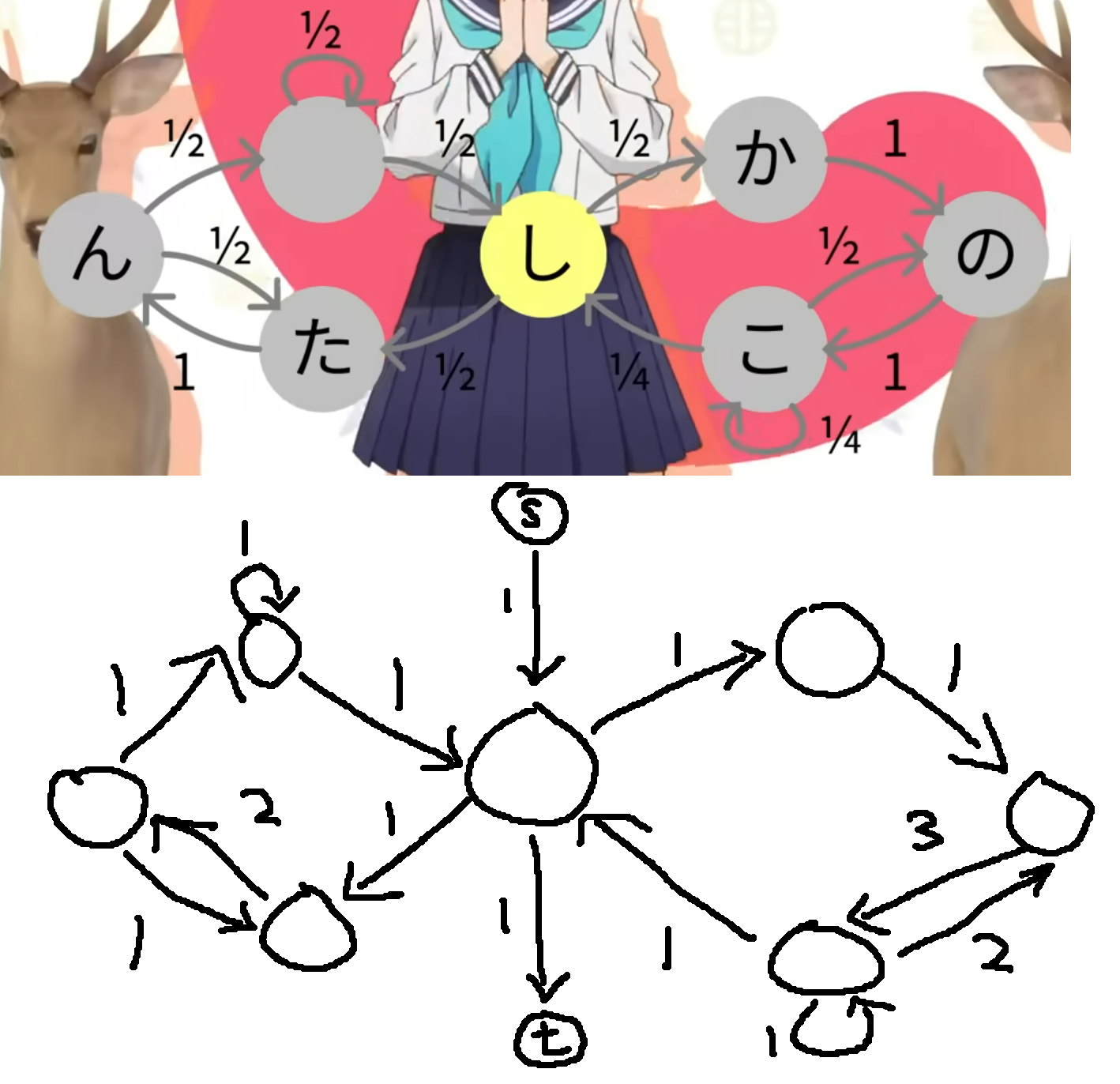
1D
I FSTed, I guess next time actually check the validation input. If it’s weak then make sure you are confident in your code.
1E
So in this problem I coded $O(\frac{n2^n}{w})$ using bitsets, but I realized that everyone just used multithreading to solve this, which was intended.
Anyways, the learning point here to use a multithreading template. I copied mine from Jeroen.
I thought I was smart so I tried to code my version which was faster in my head.
To test it, I benchmarked problem E using both my multithreading and Jeroen’s multithreading template (the actual solution code is the $O(\frac{n2^n}{w})$ written by me).
My multithreading code
#include "bits/stdc++.h"
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
const int MOD=998244353;
ll fix(ll i){
i%=MOD;
if (i<0) i+=MOD;
return i;
}
void bset(array<signed,4> &arr,int y){
arr[y/25]|=1<<(y%25);
}
int p2[105];
array<signed,4> bs2[101];
int precomp[1<<25];
struct testcase {
int TC;
int n;
string s[25];
vector<array<signed,4> > bs;
vector<int> mn;
int ans=0;
void read(int _TC){
TC=_TC;
cin>>n;
rep(x,0,n) cin>>s[x];
}
void solve(){
bs.resize(1<<n);
mn.resize(1<<n);
rep(x,1,1<<n){
if (__builtin_popcount(x)==1){
int lg=__builtin_ctz(x);
mn[x]=sz(s[lg]);
bs[x][0]=bs[x][1]=bs[x][2]=bs[x][3]=0;
rep(i,0,sz(s[lg])) if (s[lg][i]=='?') bset(bs[x],i);
}
else{
int bm=x;
int a=bm&-bm;
bm^=a;
bs[x][0]=bs[bm][0]&bs[a][0];
bs[x][1]=bs[bm][1]&bs[a][1];
bs[x][2]=bs[bm][2]&bs[a][2];
bs[x][3]=bs[bm][3]&bs[a][3];
int b=bm&-bm;
bm^=b;
mn[x]=min(mn[bm|a],mn[bm|b]);
if (__builtin_popcount(x)==2){
int lga=__builtin_ctz(a);
int lgb=__builtin_ctz(b);
rep(i,0,min(sz(s[lga]),sz(s[lgb]))) if (s[lga][i]!=s[lgb][i] && s[lga][i]!='?' && s[lgb][i]!='?'){
mn[x]=min(mn[x],i);
break;
}
}
else{
mn[x]=min(mn[x],mn[a|b]);
}
}
bs[x][0]&=bs2[mn[x]][0];
bs[x][1]&=bs2[mn[x]][1];
bs[x][2]&=bs2[mn[x]][2];
bs[x][3]&=bs2[mn[x]][3];
int curr=0;
int tot=precomp[bs[x][0]];
curr+=__builtin_popcount(bs[x][0]);
tot=(tot+p2[curr]*precomp[bs[x][1]])%MOD;
curr+=__builtin_popcount(bs[x][1]);
tot=(tot+p2[curr]*precomp[bs[x][2]])%MOD;
curr+=__builtin_popcount(bs[x][2]);
tot=(tot+p2[curr]*precomp[bs[x][3]])%MOD;
curr+=__builtin_popcount(bs[x][3]);
tot=fix(tot-(100-mn[x])*p2[curr]+1);
if (__builtin_parity(x)) ans=fix(ans+tot);
else ans=fix(ans-tot);
}
//clear the vectors!!!
bs=vector<array<signed,4> >();
mn=vector<int>();
}
void write(){
cout<<"Case #"<<TC<<": "<<ans<<endl;
}
};
vector<testcase> tests;
vector<int> idx;
void solve(int x){ //why does this work???
tests[x].solve();
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
p2[0]=1;
rep(x,1,105) p2[x]=p2[x-1]*26%MOD;
rep(x,0,101){
rep(y,0,x) bset(bs2[x],y);
}
rep(x,0,1<<25){
int curr=1;
int tot=0;
rep(bit,0,25){
if (x&(1<<bit)) curr=(curr*26)%MOD;
tot=(tot+curr)%MOD;
}
precomp[x]=tot;
}
int TC;
cin >> TC;
tests.resize(TC);
rep(x,0,TC) tests[x].read(x+1);
#ifdef DEBUG
rep(x,0,TC) solve(x);
#else
const int PARALLEL=12;
future<void> F[PARALLEL]={};
rep(x,0,TC){
bool processed=false;
while (!processed){
rep(y,0,PARALLEL){
if (!F[y].valid() || F[y].wait_for(chrono::milliseconds(0)) == future_status::ready) {
F[y] = async(launch::async,solve,x);
processed=true;
break;
}
}
}
}
bool processed=false;
while (!processed){
processed=true;
rep(y,0,PARALLEL){
if (F[y].valid() && F[y].wait_for(chrono::milliseconds(0)) != future_status::ready) {
processed=false;
break;
}
}
}
#endif
rep(x,0,TC) tests[x].write();
}
Jeroen’s multithreading code
#include "bits/stdc++.h"
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
const int MOD=998244353;
ll fix(ll i){
i%=MOD;
if (i<0) i+=MOD;
return i;
}
void bset(array<signed,4> &arr,int y){
arr[y/25]|=1<<(y%25);
}
int p2[105];
array<signed,4> bs2[101];
int precomp[1<<25];
struct testcase {
int TC;
int n;
string s[25];
vector<array<signed,4> > bs;
vector<int> mn;
int ans=0;
void read(int _TC){
TC=_TC;
cin>>n;
rep(x,0,n) cin>>s[x];
}
void solve(){
bs.resize(1<<n);
mn.resize(1<<n);
rep(x,1,1<<n){
if (__builtin_popcount(x)==1){
int lg=__builtin_ctz(x);
mn[x]=sz(s[lg]);
bs[x][0]=bs[x][1]=bs[x][2]=bs[x][3]=0;
rep(i,0,sz(s[lg])) if (s[lg][i]=='?') bset(bs[x],i);
}
else{
int bm=x;
int a=bm&-bm;
bm^=a;
bs[x][0]=bs[bm][0]&bs[a][0];
bs[x][1]=bs[bm][1]&bs[a][1];
bs[x][2]=bs[bm][2]&bs[a][2];
bs[x][3]=bs[bm][3]&bs[a][3];
int b=bm&-bm;
bm^=b;
mn[x]=min(mn[bm|a],mn[bm|b]);
if (__builtin_popcount(x)==2){
int lga=__builtin_ctz(a);
int lgb=__builtin_ctz(b);
rep(i,0,min(sz(s[lga]),sz(s[lgb]))) if (s[lga][i]!=s[lgb][i] && s[lga][i]!='?' && s[lgb][i]!='?'){
mn[x]=min(mn[x],i);
break;
}
}
else{
mn[x]=min(mn[x],mn[a|b]);
}
}
bs[x][0]&=bs2[mn[x]][0];
bs[x][1]&=bs2[mn[x]][1];
bs[x][2]&=bs2[mn[x]][2];
bs[x][3]&=bs2[mn[x]][3];
int curr=0;
int tot=precomp[bs[x][0]];
curr+=__builtin_popcount(bs[x][0]);
tot=(tot+p2[curr]*precomp[bs[x][1]])%MOD;
curr+=__builtin_popcount(bs[x][1]);
tot=(tot+p2[curr]*precomp[bs[x][2]])%MOD;
curr+=__builtin_popcount(bs[x][2]);
tot=(tot+p2[curr]*precomp[bs[x][3]])%MOD;
curr+=__builtin_popcount(bs[x][3]);
tot=fix(tot-(100-mn[x])*p2[curr]+1);
if (__builtin_parity(x)) ans=fix(ans+tot);
else ans=fix(ans-tot);
}
//clear the vectors!!!
bs=vector<array<signed,4> >();
mn=vector<int>();
}
void write(){
cout<<"Case #"<<TC<<": "<<ans<<endl;
}
};
vector<testcase> tests;
const int PARALLEL=12;
void paralleltests(int l=0, int r=PARALLEL-1) {
if (l==r) {
for(int i=l;i<(int)tests.size();i+=PARALLEL) {
tests[i].solve();
}
return;
}
ll mid = (l+r)/2;
auto handle = std::async(launch::async,paralleltests, l,mid);
paralleltests(mid+1,r);
handle.wait();
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
//initialization code goes here
int TC;
cin >> TC;
tests.resize(TC);
rep(x,0,TC) tests[x].read(x+1);
#ifdef DEBUG
rep(x,0,TC) tests[x].solve();
#else
paralleltests();
#endif
rep(x,0,TC) tests[x].write();
}
I am testing using AMD Ryzen 7 3700X that has 8 cores and 16 threads.
| PARALLEL | My multithreading (s) | Jeroen Multithreading (s) |
|---|---|---|
| 1 | 121.856 | 122.584 |
| 2 | 85.572 | 71.149 |
| 4 | 50.138 | 40.726 |
| 8 | 31.020 | 26.938 |
| 12 | 26.871 | 25.538 |
Turns out I don’t know how to optimize code… Jeroenosity!
Here is the template for MHC I have modified from his code.
Remember to compile with -lpthread flag!
#include "bits/stdc++.h"
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
struct testcase {
int TC;
void read(int _TC){
TC=_TC;
}
void solve(){
}
void write(){
cout<<"Case #"<<TC<<": ";
}
};
vector<testcase> tests;
const int PARALLEL=12;
void paralleltests(int l=0, int r=PARALLEL-1) {
if (l==r) {
for(int i=l;i<(int)tests.size();i+=PARALLEL) {
tests[i].solve();
}
return;
}
ll mid = (l+r)/2;
auto handle = std::async(launch::async,paralleltests, l,mid);
paralleltests(mid+1,r);
handle.wait();
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
//initialization code goes here
int TC;
cin >> TC;
tests.resize(TC);
rep(x,0,TC) tests[x].read(x+1);
#ifdef DEBUG
rep(x,0,TC) tests[x].solve();
#else
paralleltests();
#endif
rep(x,0,TC) tests[x].write();
}
2A
I knew how to calculate the maximum number of possible numbers for the hard version. I thought it would be very big, so I coded a very ugly MITM. But after I ran my code I realized that the answer was actually about 70 million… I could have saved myself alot of trouble (and probably my round 3 qualification) if I just wrote the stupid brute force.
2B
I FSTed this problem. Honestly, I think it is a fair FST, I did not a consider a case that almost everyone didn’t consider.
ggwp Meta
2C
I am abit salty on this. Instead of coding $O(RC \log ^3)$ like most people, I coded $O(RC \sqrt{RC})$ instead.
Given some color $c$, we want to calculate the frequency array of distance for each pairwise cell with the same color.
So I split into $2$ cases, $occ \leq B$ and $occ > B$.
Now, for some reason I set $B = RC$ during validation (???). So when I was running the full testset, I realized my code was taking super long because of that (the time complexity was $O((RC)^2)$. So I quickly changed $B=800$ to save it. Then I realized this means I totally didn’t test the part of my code that had $occ > B$. So I changed $B=400$ and made sure that the outputs matched. It matched so I submitted my code.
Then after systests were finished, my code got WA. I realized my code for the $occ>B$ case was totally wrong (I wrote += instead of -= for the part which minuses the frequency from the same color). This literally could have been avoided if I had set $B=0$ and tried it on the validation test, but I was too lazy (and stressed) to do so. But this means that in the full test, there was no such test case where $occ \in (400,800]$. men,,,,,,,
P.S. My friend dantoh was first blood on this. Congrats to him!