Notes on RSA
Taking CS2107 this semester.
In the slides for RSA, it makes the claim that for any $m,r,n$, we have $m^r \mod n = m^{r \mod \phi(n)} \mod n$.

This is obviously bullshit for any values of $m,r,n$. The top of the slide did assume that $m<n$, so let’s also assume that $1 \leq m < n$. And let’s also be nice and assume that $n=pq$.
But even with that stronger constraint, this is still not generally true. We still need the constraint that $\gcd(m,n)=1$, so that this is true by Euler’s theorem.
Otherwise, a very simple example is to take $m=2,n=6,r=2$. Then $m^r \mod n = 2^2 \mod 6 = 4$ and $m^{r \mod \phi(n)} \mod n = 2^{2 \mod 2} \mod 6 = 1$.
But I guess you can argue that we should never send a plaintext with $\gcd(m,n) \neq 1$. Otherwise, the attacker can calculate $\gcd(c,n) = \gcd(m^e,n) \neq 1$ and obtain the private key.
And we probably don’t need any safeguards against the case against encoding plaintext with $\gcd(m,n)!=1$, because that is extremely unlikely. Because the probability is about the same as the attacker randomly guessing a multiple of a factor of $n$ anyways, which we want to claim is extremely unlikely.
But anyways, the funny thing is that even when $\gcd(m,n) \neq 1$ and $n=pq$, we can still claim a weaker version of $m^r \mod n = m^{r \mod \phi(n)} \mod n$.
Specifically, that $m^r \mod n = m^{r + \phi(n)} \mod n$ for $r \geq 1$.
I think this problem is related to https://judge.yosupo.jp/problem/tetration_mod, where we only need the weaker claim that the result is true for $r \geq n$, without assuming any property of $n$, but I’m pretty sure $r \geq \log_2(n)$ suffices, which probably should be $r \geq \max_p \lceil \frac{v_p(n)}{v_p(m)} \rceil$.
Note that when $n=pq$, or even when $n$ is squarefree, $1 \geq \max_p \lceil \frac{v_p(n)}{v_p(m)} \rceil$ since $1 \geq v_p(n)$.
The general idea of the proof is that if we we have $n = p^a q^b w$ ($w$ is some composite number coprime with $p$ and $q$) and $m = p^{a’} q^{b’}$, then eventually, $m^i$ will be a multiple of $p^a q^b$ and we claim that it stays within the set of $p^aq^b (\mathbb{Z}/w\mathbb{Z})^\times = {p^aq^bx \mid \gcd(x,w)=1 } $.
This set is also a group where multiplication is defined under modulo $n$.
We will very liberally use the fact that $xay \mod ab = a (xy \mod b) \mod ab$.
By the way, the identity of this group isn’t that trivial. Let $z$ be the integer such that $p^aq^bz = 1 \mod w$, which exists since $w$ and $p^aq^b$ are coprime by definition. Then $p^aq^bz$ is the identity of the group.
This is kind of annoying to work with. But the group is isomorphic to $(\mathbb{Z}/w\mathbb{Z})^\times$ anyways. Just mod everything by $w$ to get the mapping.
Anyways, the point is that order of the group is $\phi(w)$ and $\phi(w) \mid \phi(n)$ since $w \mid n$.
So, for $m^r \mod n = m^{r + \phi(n)} \mod n$, we just need large enough $r$ such that $m^r$ is inside the target group, which is given by $\max_p \lceil \frac{v_p(n)}{v_p(m)} \rceil$.
Btw I asked ChatGPT5 to prove that if $d \mid n$ then $\phi(d) \mid \phi(n)$ and it gave me https://chatgpt.com/share/68c3baa5-06ec-8007-b0dd-6eea8f72abef. PhD level reasoning btw.
On this topic, inside some quiz, there was a question.
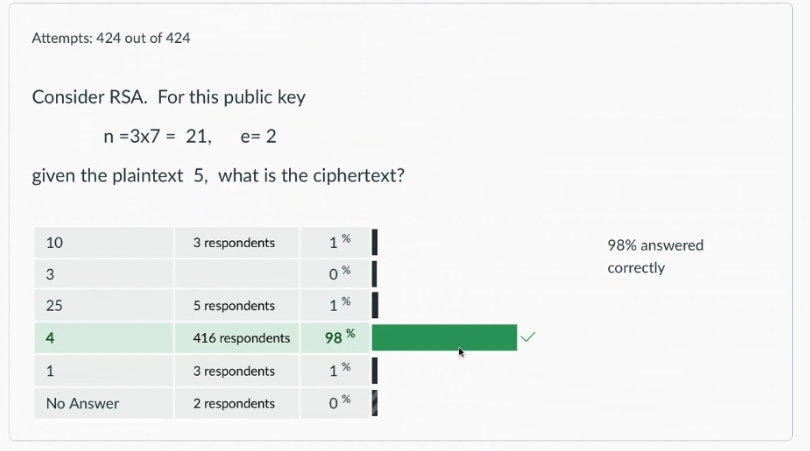
Mechanically, we have $c = m^e \mod n = 4$.
However, we also have that $\phi(n) = 2 \times 6$ and $e$ are not coprime.
It was MRQ as the options choice, so you are allowed to choose nothing.
So are you supposed to choose $4$ or nothing in this case?
Surely, the algorithm to generate the cipher text from the plaintext is well-defined. But you just cant get back to the plaintext.
Luckily, I decided to choose $4$ for some reason. But I was very worried that you were supposed to choose nothing anyways.
But apparently I was overthinking because when going through this quiz, the professor only said “This one ok, probably mistake. Careless mistake.” So I guess he didn’t even consider that the decryption algorithm doesn’t even exist….
It is very annoying to have to read professor’s mind in these types of cases.
In MA1522 there was a question like if $A$ is $n \times m$ matrix and $B$ is $m \times n$ matrix, is $\text{det}(AB) = \text{det}(A) \text{det}(B)$?
And you are supposed to answer false because you have to read professor’s mind to know that “lol the determinant is only defined for square matrices”? The actual answer is false because of that stupid reason.