AP Stats Crib Notes
ASSOCIATION DOES NOT IMPLY CAUSATION
Boilerplate
Describe Distribution
- Mode: peak of a distribution. Unimodal if one peak, bimodal if two peak
- Shape: Symmetric if values are mirror image around midpoint. Otherwise, skewed to left if spreads towards small values, skewed to right if spreads towards large value. Additionally, bell-shaped if symmetric with center mound and two sloping tails
- Center: median of a distribution
- Spread: range or IQR
- Outliers: extreme values in the distribution
- Clusters & Gaps: clusters are subgroups that values fall into, gaps are holes which no values fall into
Example answers:
The histogram of dissolved oxygen concentration in Alaskan streams with water temperatures colder than 8°C is unimodal and skewed left with a median between 11 and 12 mg/l. The first quartile is in the bin from 10-11 mg/l and the third quartile is in the bin from 12-13 mg/l , so the IQR is approximately 2 mg/l. There do not appear to be any high outliers, but there are several potential low outliers because the values in the 2-3, 4-5, and 5-6 bins are all certainly more than 1.5 IQR below the first quartile.
Describe Difference in Distribution
- Center: compare the center of the distributions directly
- Spread: indicates differences in spread between both distributions
Example answers:
If the researchers’ belief is correct, then streams with water temperature colder than 8℃ are healthier for wildlife. The distribution of dissolved oxygen concentration for colder streams has a higher center because its median (between 11 mg/l and 12 mg/l) is larger than the median for warmer streams (5.43 mg/l). The shape of the distribution of dissolved oxygen concentration for colder streams is different from the shape of the distribution for warmer streams. The distribution of values of dissolved oxygen concentration for colder streams is skewed to the left but the distribution of values for warmer streams is skewed to the right. Both distributions have a similar spread because they both have similar IQR values — approximately 2 mg/l for the colder streams and 1.73 mg/l for the warmer streams.
Describe Linear Relationship Scatterplot Graph
- Direction: increasing or decreasing
- Strength of association: strong or weak
- Form of association: linear, approximately linear, non-linear
- Unusual features: outliers
Example answer:
The scatterplot reveals a strong, positive, roughly linear association between the chest circumference and weight of tule elk. There are no points that seriously deviate from the straight-line pattern of the points in the plot.
The scatterplot reveals a strong, positive, roughly linear association between the mass and length of bullfrogs. There are no points that seriously deviate from the straight-line pattern of the points in the plot.
Describe Appropriate Experimental Method for Randomization
Number the 60 driveways from 01 to 60. Using a random number generator, generate two-digit integers between 01 and 60. Ignore 00 and any number greater than 60 until 30 unique numbers are obtained. Assign the driveways with those 30 unique numbers to receive concrete with fibers and the remaining 30 driveways to receive concrete without fibers.
For each pair of twins, label one person as twin A and label the other person as twin B. For each pair of twins, toss a coin. If the coin lands on heads, twin A gets the placebo and twin B gets the active drug. If the coin lands on tails, twin A gets the active drug and twin B gets the placebo.
Hypothesis Testing
Let $\mu_d$ represent the true mean difference (placebo minus omega-3) of irritability scores for all people with this medical condition.
The null hypothesis is $H_0 : \mu_d = 0$ and the alternative hypothesis is $H_a : \mu_d > 0$.
The appropriate inference procedure is a matched pairs t-test for a mean difference.
The independence condition for performing a paired t-test for a mean difference is satisfied because the data were obtained from a randomized experiment where the week in which the patient received the treatment was randomly assigned.
The sampling distribution of the mean difference must be approximately normal. Although the sample size is less than $30$ ($n=19$), this is satisfied because the boxplot for the sample differences shows an approximately symmetric distribution with no outliers.
The corresponding p-value is $\approx 0.0028$. Because the p-value is less than he significance level, $\alpha \approx 0.05$, the null hypothesis should be rejected. The data provide convincing statistical evidence that for patients similar to those in the study, the true mean difference (placebo minus omega-3) in irritability scores for people with this medical condition is greater than zero. This suggests the omega-3 fatty acids are helpful in reducing irritability scores in people with this medical condition.
Confidence Interval
The appropriate procedure is a one-sample z-interval for the proportion of all teenagers in the United States who would respond that they use a video streaming service every day.
This survey selected a random sample of 920 teenagers in the United States, which enables the interval to be generalized to the population of interest. This sample of 920 teenagers is less than 10% of the total number of teenagers in the United States, which is required as sampling was conducted without replacement from a finite population. In addition, there were more than 10 successes and 10 failures as (920)(0.59) = 542.8 (or 543) responded that they use a streaming service daily and (920)(0.41) = 377.2 (or 377) responded that they did not. Thus, the sample size is large enough to support the assumption that the sampling distribution of $\hat p$ is approximately normal.
Therefore, a 95% confidence interval is given by $0.59 \pm 0.032$ which is $(0.558,0.622)$.
We can be 95% confident that the proportion of all teenagers in the United States who would respond that they use a streaming service every day is between 0.558 and 0.622.
Displaying Data
For AP exams, all displays must be clearly labelled and titled or else AP would subtract points.
For categorical data, we have the following visualizations:
- pie chart, used when emphasize each category’s relation to the whole
- bar graph, height is used to represent size of each category, can easily compare categories
- dot plot, frequency of each category is measured by number of dots
If there are 2 different sets of categorical data $A$ and $B$, we can write a two-way table where we list out the number of elements in each category $(a,b)$ for $a \in A$ and $b \in B$.
For example,
| $a_1$ | $a_2$ | total | |
|---|---|---|---|
| $b_1$ | 10 | 20 | 30 |
| $b_2$ | 30 | 40 | 70 |
| total | 40 | 60 | 100 |
We can also represent the information in a bar chart. For example we can have two bars $a_1$ and $a_2$ that are both the same height that allows us to compare the proportion of $b_1$ and $b_2$ between them. Alternatively, we can just have $4$ bars, one for each possible category.
For quantitiative data, we have the following visualizations:
- stemplots, remember to explictly write the key i.e. “6|3 represents a 63kg boy”, to simplify data, you can round values, try to aim for 5 stems minimum, ensure each stem has same number of possible leaf digits
- histograms, $y$-axis can represent either or both relative and total frequencies, all classes should be the same width, good to calculate frequency table before drawing histogram
- relative cumulative frequency plots (ogive), we can tell what value is the $p$-th percentile and also figure out the percentile of some value
Describing a Graphical Display
Mean and median are both measures of the “centers” of the dataset. If there is a even number of elements, the median is the average of the 2 middle numbers.
The mean is affected significantly by outliers but the median is not, so we call the median a resistent measure.
The $p$-th percentile of a distribution is the value such that $p$ percent of the observations is $\leq $ it.
Range and IQR (difference between $Q_3$ and $Q_1$) are both measure of the spread. Range is affected a lot by outliers.
We can use a boxplot to show the min, $Q_1$, median, $Q_3$ and max of a distribution. A modified boxplot is a boxplot that plots all outliers individually. The rule of being an outlier is that it falls more than $1.5$ IQR away from the left of $Q_1$ or the right of $Q_3$.
Designing Studies and Experiments
An observational study does not impose any treatment on the individuals, but in an experiment, we do. Because of this, observational studies often have lurking variables, for example people who eat more vegetables are have lower cholestrol, since they tend to live healthier lifestyles.
An experimental unit (subjects if humans) is the smallest unit to which a treatment is applied. The specific experimental condition applied to units are called treatments. Experiments want to reveal response when changing variables. We can have multiple variables, known as factors or explanatory variables, and each factor can take multiple specific values, called levels. Then, we will measure the response variables.
A well-designed experiment must have:
- control, effort to minimize variability within subjects, eliminate lurking variables
- replication, each experimental unit has its own variability, so each treatment group should have multiple treatment units, we cannot eliminate chance variation, but we can reduce it
- randomization, use chance to make assignment so that we can assume treatment groups are essentially similar, and no systematic differences between them
In a randomized comparative experiment, we split experimental units into 2 groups randomly and then apply different treatment to each group.
Before doing randomized assignment, we can also do block design where we split the participants into blocks where we think the variation within each block would be less than the variation between blocks. Some examples blocks are gender, race and age.
Matched pairs design is a more specific example of blocked designed where we match subjects so that each pair of subjects are as similar to each other as possible. Note that a common variation of the matched pairs design is for each person to have both treatments imposed on them, so that they become the control for themselves.
A reason for doing block design is to mitigate simpson’s paradox where a trend that appears in two different groups of data reverse when put together.
| Treatment A | Treatment B | |
|---|---|---|
| Not Serious | 81/87 (93%) | 234/270 (87%) |
| Serious | 192/263 (73%) | 55/80 (69%) |
| Both | 273/350 (78%) | 289/350 (83%) |
As shown above, treatment A is superior to treatment B when comparing in each group individually. But when both groups are put together, treatment B seems superior.
Another thing to note during experiments is the placebo effect where the act of imposing a treatment of experimental units changes the response. Note that even the researchers are susceptible to the placebo effect if the response is subjectively determined by the researchers. To combat this, we can use blinding, where we deny the participants knowledge of which treatment they are receiving. A double-blind experiment is one where the research is also unaware of which treatment participants are receiving. However, sometimes double-blind experiments are simply impossible due to lack of realism. This lack of realism also does not allow us to apply the conclusions from the experiments into more general. Statistical analysis cannot tell us how far the results will generalize to other settings.
Types of bias:
- Response bias: when polled answer is not reported accurately
- Voluntary response bias: will tend to get strong opinions
- Non-response bias: comes hand in hand with voluntary response bias
- Undercoverage bias
Hypothesis Testing
Type 1 error: false positive (probability $\alpha$ is $p$-value of the test) Type 2 error: false negative (probability is $\beta$, we need population mean to calculation)
Power of a test is defined as $1 - \beta$. We can increase it by:
- decreasing $\alpha$
- increasing sample size
- decrease $\sigma$
- consider alternative hypothesis that is further away from $\mu_0$
Normal Distribution
- $E(aX) = aE(X)$
- $E(X \pm Y) = E(X) \pm E(Y)$, $X$ and $Y$ need not be independent
- $\text{Var}(aX) = a^2 \text{Var}(X)$
- $\text{Var}(X \pm Y) = \text{Var}(X) + \text{Var}(Y)$, if $X$ and $Y$ are independent
Normal distribution z-score: $\frac{z - \mu}{\sigma}$
A sample statistic is a quantity calculated from values in a sample, used for estimating a value of a population parameter.
A sampling distribution is unbiased if the expected value of it is the population parameter. Otherwise, it is called biased.
Confidence Intervals
First, suppose that $\sigma$ is known.
Conditions:
- SRS
- Normality: either original distribution is normal or $n \geq 30$.
- Independence: population size is at least $10$ times the sample size
The confidence interval is $\bar x \pm z^* \frac{\sigma}{\sqrt n}$. $\bar x$ is referred to as the point estimate and $z^* \frac{\sigma}{\sqrt n}$ is referred to as the margin of error.
If $\sigma$ is not known.
Conditions:
- Random: SRS
- Normality: population is normal or distribution is symmetric and single-peaked and sample size is not very small
- Independence: population size is at least $10$ times the sample size.
The confidence interval is $\bar x \pm t^* \frac{\sigma}{\sqrt n}$. The interval is exactly correct when population distribution is normal and approximately correct when $n$ is large.
Population Proportion
Suppose a population has $p$ chance of being $1$ and $1-p$ change of being $0$. Then, $\mu=p$ and $\sigma = \sqrt{p(1-p)}$.
Conditions:
- Random: SRS
- Normality: $n \cdot \max(p,1-p)$ is at least $10$.
- Indepence: population size is at least $10$ times the sample size
The confidence interval is $\hat p \pm z^* \sqrt{\frac{\hat p (1 - \hat p)}{n}}$
z-score: $\frac{\hat p - p_0}{\sqrt{\frac{p_0(1-p_0)}{n}}}$, if we want to test $H_0: p = p_0$.
Two-Sample Problems
If we have a sample of size $n_1$ from $N(\mu_1, \sigma_1)$ and a sample of size $n_2$ from $N(\mu_2, \sigma_2)$, then the z-score is $z=\frac{\bar x_1 - \bar x_2 - (\mu_1 - \mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}$.
If we do not know $\mu$ and $\sigma$, we will calculate the $t$-score as $t=\frac{\bar x_1 - \bar x_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}$ with distribution $t(n-1)$, if we want to test $H_0: \mu_1 = \mu_2$.
The degree of freedom for $t$-distribution if given by:
- conservative estimate: $\min(n_1,n_2)-1$
- Welch and Satterthwaite approximation: use GC
Conditions:
- Random: SRS
- Normality: population distributions have similar shapes and the data have no strong outliers
- Independence: both samples are independent from each other and respective population size is at least $10$ times respective sample sizes
For two-sample proportion, the z-score is $z=\frac{\hat p_1 - \hat p_2}{\sqrt{\frac{\hat p_1 (1- \hat p_1)}{n_1} + \frac{\hat p_2 (1- \hat p_2)}{n_2}}}$
To test $H_0 : p_1 = p_2$, it is a bit different. First, we calculate $\hat p_c = \frac{X_1+X_2}{n_1+n_2}$ as the weighted average of $\hat p_1$ and $\hat p_2$. Then, the z-score is $z=\frac{\hat p_1 - \hat p_2}{\sqrt{\hat p_c (1- \hat p_c)(\frac{1}{n_1}+\frac{1}{n_2})}}$
Regrssion Analysis
Conditions:
- Linear: scatterplot is roughly linear, check to see that residuals are roughly centered
- Independent: population size is at least $10$ times larger than sample size
- Normal: check that plot of residuals is approximately normal, no clear skewness
- Equal Variance: the variance of residual plot should be roughly the same for each $x$-value
- Random: SRS
The regression line is represented by $\hat y_i = \alpha + \beta x_i$. $\alpha$ is known as the $y$-intercept and $\beta$ is known as the slope.
The residual is denoted by $r_i = y_i - \hat y_i$.
This is a computer printout between hours a student study and their caffeine intake in mg.
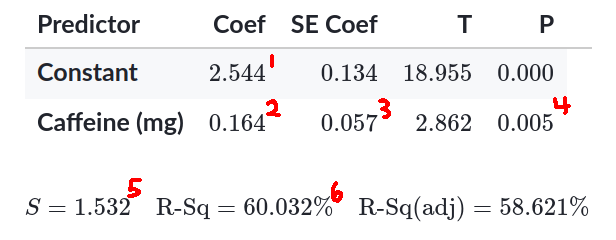
- The regression line is $\hat y = v_1 + b \cdot v_2$
- When caffine intake intake is $0$ mg, the study time is predicted to be $v_1$ hours
- For every $1$ mg in caffeine, the study time is predicted to increase by $v_2$ hours
- The confidence interval of the slope of the true regression line is given by $v_2 \pm t^* v_3$, where $t^*$ is the critical value of the $t(n-2)$ density curve
- The P-value given as $v_4$ is for the hypothesis hypothesis $H_0 : \beta =0$
- $v_5$ is the standard deviation of the residuals, which measures the size of the typical prediction error in the residuals
- $v_6$ is the percentage of variation in the values of $y$ that is explained by the regression line
Chi Squared Test
Suppose a distribution has $k$ discrete outcomes.
Conditions:
- Random: SRS
- Independent: population size is at least $10$ times larger than sample size
- Large sample size: all the expected counts are at least $5$
The chi-squared test statistic is $X^2 = \sum \frac{(O-E)^2}{E}$, where $O$ is the observed count and $E$ is the expected count.
Then $X^2$ is approximate a $\chi^2$ distribution with $k-1$ degrees of freedom.
$H_0$: the actual population proportions are equal to the hypothesized proportions
$H_a$: at least one of the actual population proportions differ from the hypothesized proportions
The p-value is $P(\chi^2 > X^2)$.
If we have $r$ objects and each object has $c$ different discrete outcomes, we can do a test for homogeneity of populations. Everything is same as above except that we have $(r-1)(c-1)$ degrees of freedom.