Akari Strategy
I have been playing Daily Akari, well, daily for the past few months. I usually get stuck on more harder puzzles. I think this is a technique I can use more to get unstuck. Although, idk how to use this technique quickly. My boyfriend is way too good at akari. I have no idea how his brain works… Maybe he is a chad shape rotator and I am simply a stupid wordcel.
Pretty much the entire idea of this technique is to find a set of lines and a set of blocks, such that each blocks adjacent empty squares contain some line. Then for each line, figure out the maximum value a point on each line can contribute. If the values of lines and blocks are the same, then we must always take the maximum value on each line.
Examples are below (in approximate order of difficulty).
Note that $(x,y)$ denotes the cell on the $x$-th row and $y$-th column.
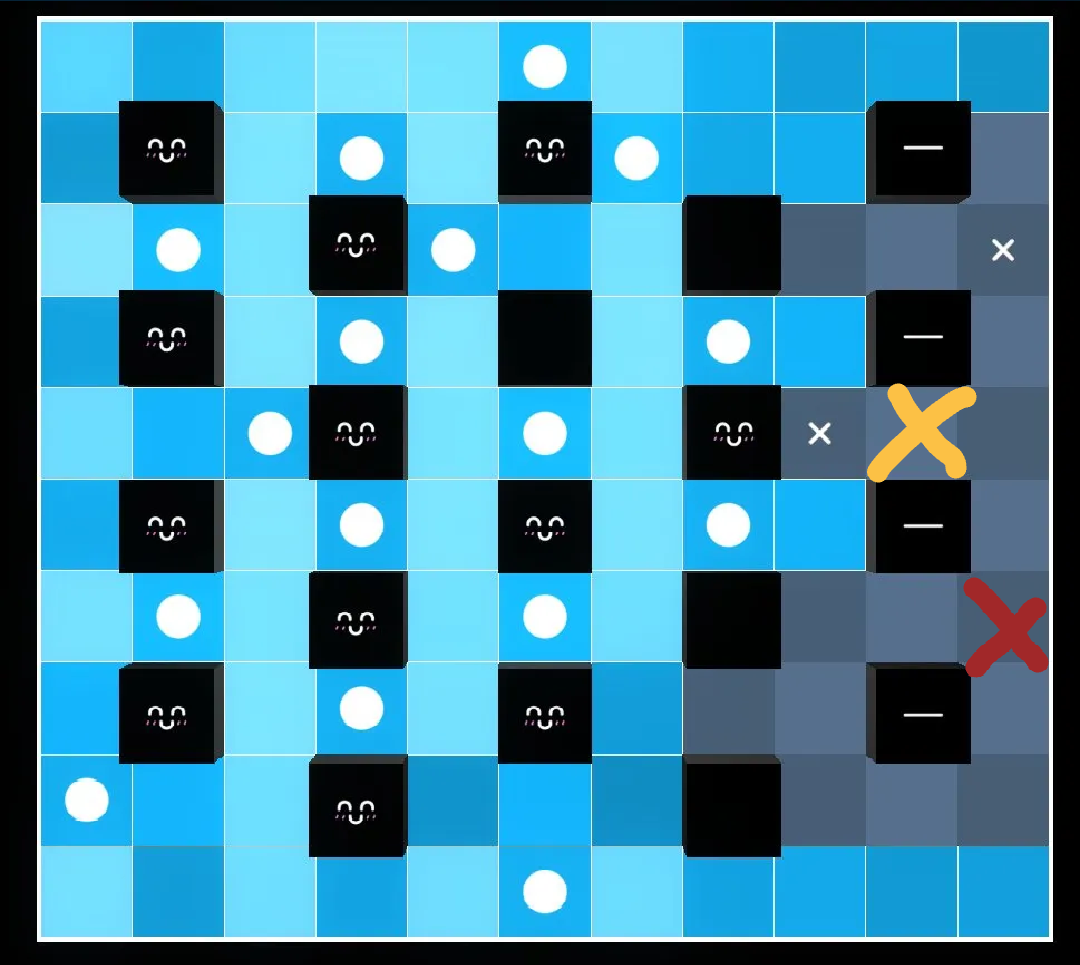
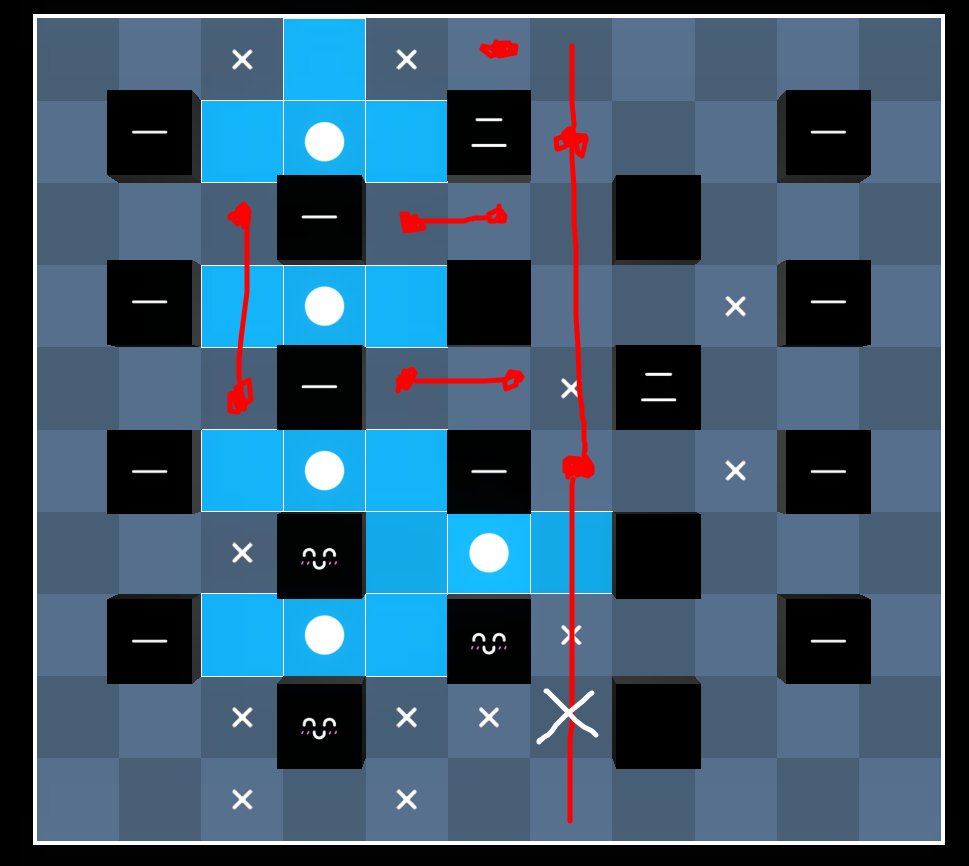
Daily Akari 277
Draw the following lines. They all have value $1$. The total value of the lines is $7$ and so are the value of the blocks.

Therefore, we must put an akari on on cells $(4,3)$ and $(5,2)$ since only those cells add value $1$ to their respective lines. Then subsequencely, we must put an akari on cell $(5,6)$.
This is enough to solve the rest of the puzzle.
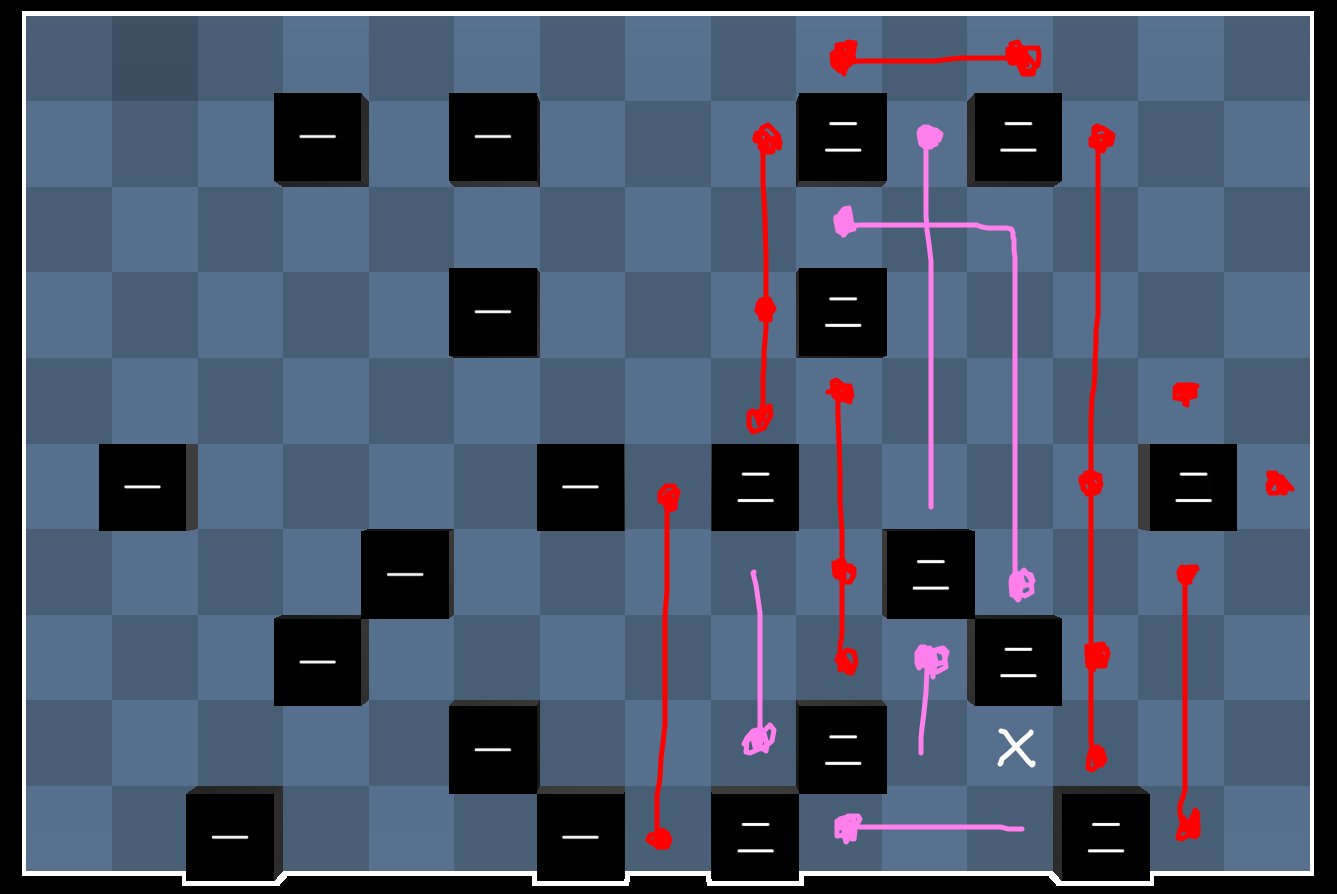
Daily Akari 112
Draw the following lines. The red lines all have value $1$, while the pink lines all have value $2$. I have drawn the only places where akaris should be placed on each line. The value of lines and blocks is $20$. So we can already deduce that we should place all the pink dots. This is enough to solve the puzzle.
Note that we had to deduce first that $(9,12)$ cannot have an akari.
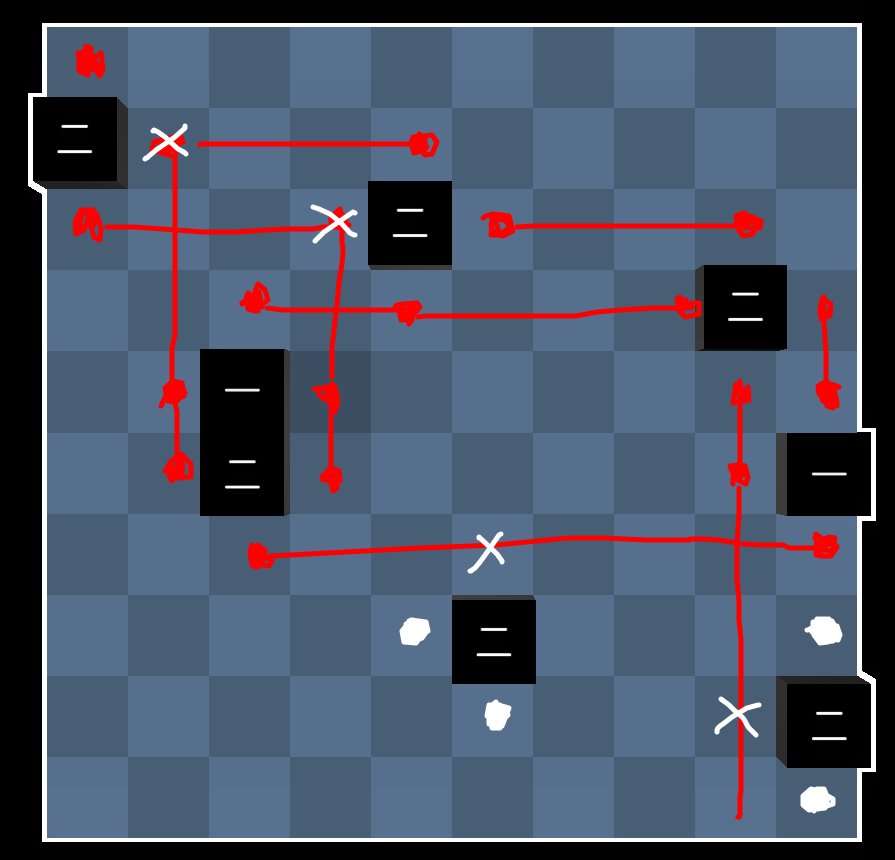
Daily Akari 63
Draw the following line that all have value $1$.
Note that we can deduce that there are no akaris on $(2,2)$ and $(3,4)$ since they intersect two lines.
We can also deduce that there are no akaris on $(7,6)$ and $(9,9)$ since they intersect a line without increasing any relavant block values.
This information is enough to solve the puzzle.
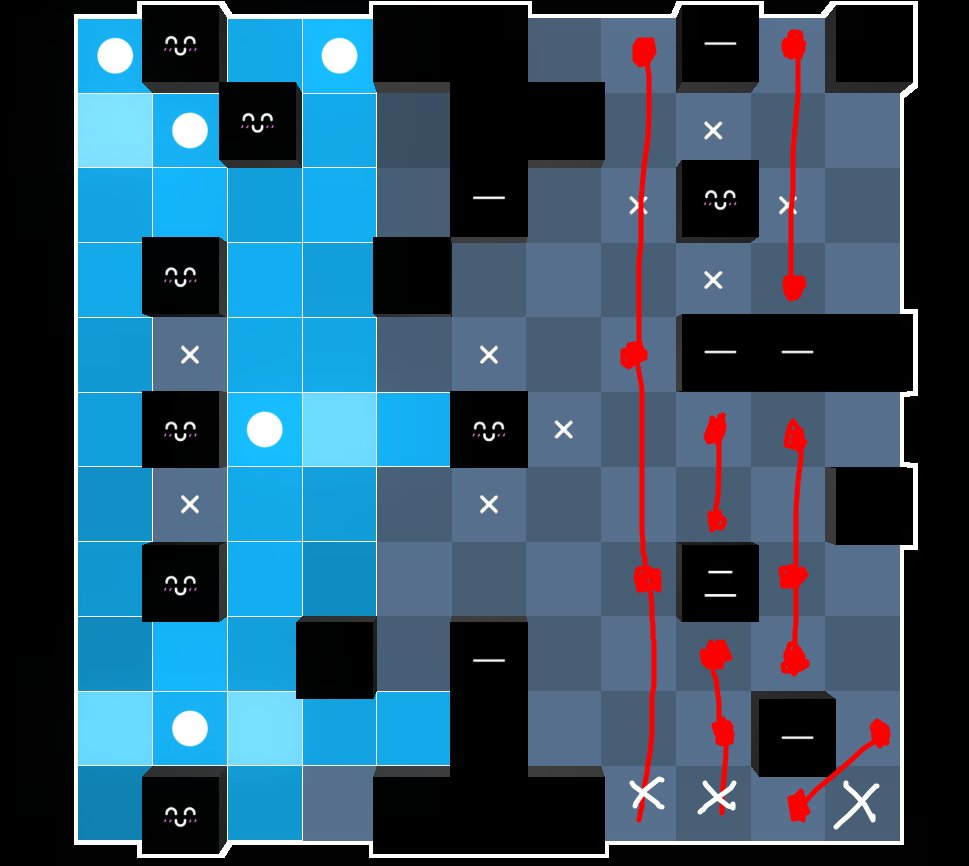
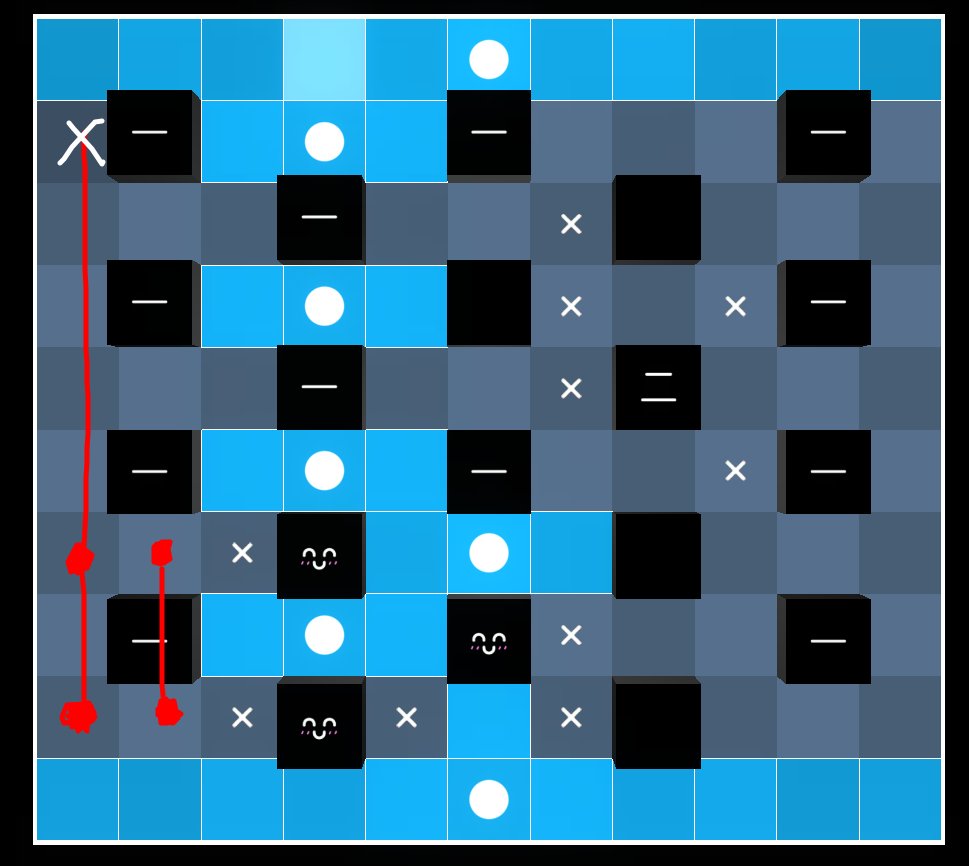
Daily Akari 278
Note that the bottom red line is due to both point being around the $1$ block, which also allows us to deduce that $(11,10)$ is not an akari.
The next move is to put an akari on $(11,9)$.
Daily Akari 229
This puzzle was set by Nachia, very nice puzzle. Apparently he is going to compete in ICPC yokohama regionals this year. I am so fucked. Going to meet Chung-Chun in ICPC Taichung too …
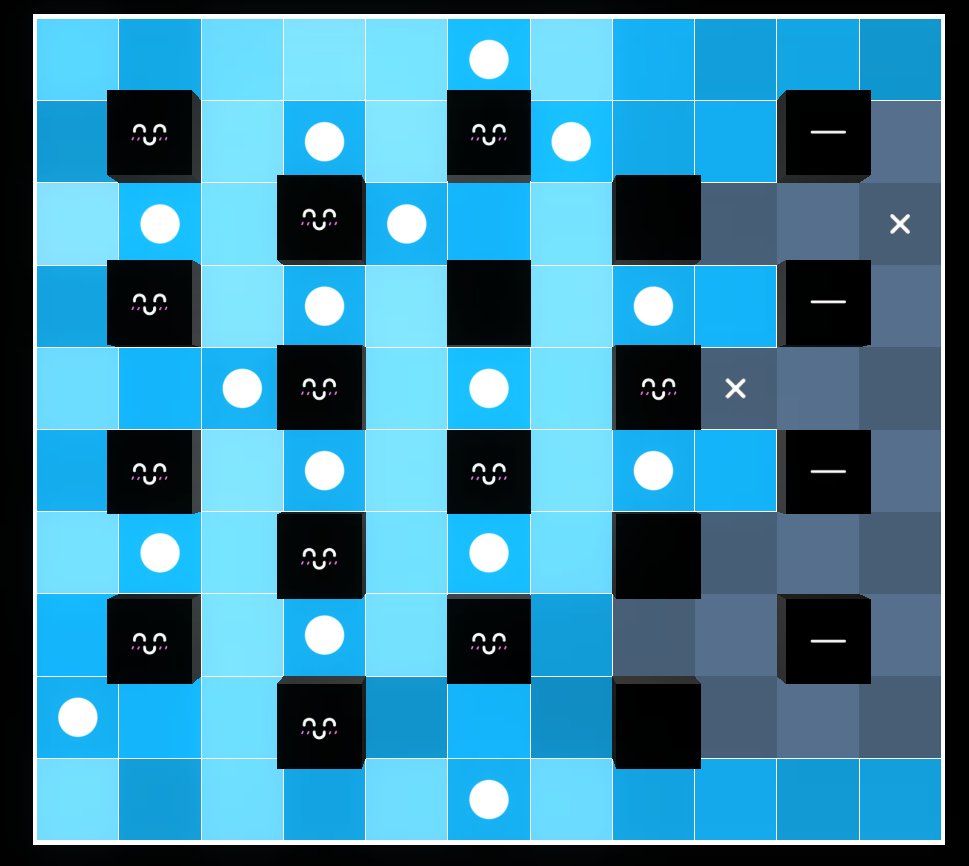
Note sure how to solve this last step without mental dfs on the 2 cases of the top $1$. But I guess the technique in this blog is also very mentally demanding…
EDIT: My boyfriend told me its deduce that $(7,11)$ doesn’t contain an akari (I guess by dfs), then again deduce that $(5,10)$ doesn’t contain an akari (again by dfs)… doesn’t seem that much simpler…