The Devil’s Algorithm
This was a project I did back in 2022. I uploaded the CP version of it to codebreaker at https://codebreaker.xyz/problem/devil. This blog will be the editorial I guess?
I would like to thank Ling Yan Hao for mentoring me for this project.
All code used for this project is found in this github repo. Do not ask me for documentations. I wrote these codes almost 3 years ago.
There was a period of time before I found out about competitive programming where I was interesting in twisty puzzles. I have quite an extension collection of twisty puzzles. There are probably more but my sister probably took them.

So obviously along the way, I had to have stumbled across some Devils’ Algorithm. I knew about the Devil’s Algorithm for the floppy cube and also this April Fool’s Video for 3x3 Devil’s Algorithm.
I decided to tackle this problem for my high school research project. I solved it in a few days… stupidest research.
Let $R_ n$ denote the $n \times n \times n$ Rubik’s Cube for brevity.
Anyways, let’s first define what a Devil’s Algorithm is first. First, we need to define what a valid “move” is on a Rubik’s Cube. I will use the quarter slice turn metric. So for $R_ n$, we have $6n$ possible moves. There are $6$ faces on a Cube which we denote Up, Left, Front, Right, Bottom, Down. Then each move will be notated $\texttt{X}_ i$ or $\texttt{X}_ i’$ ($1 \leq i \leq N$), where $\texttt{X} \in \{\texttt{U},\texttt{L},\texttt{F},\texttt{R},\texttt{B},\texttt{D}\}$, for the clockwise and anti-clockwise 90 degrees turn of the $i$-th layer from the top if the $\texttt{X}$-th face was orientated to the top. Notice that we only have $3n$ distinct possible moves because we would have the same set of moves if $\texttt{X} \in \{\texttt{U},\texttt{L},\texttt{F}\}$. For example, $\texttt{U}_ i$ is the same move as $\texttt{D}_ {N-i+1}’$.
Given a sequence of moves $s_ 0,s_ 1,\ldots,s_ {k-1}$, we define $p_ j$ as the state after doing $j$ moves $s_ {0 \% k}, s_ {1 \% k}, \ldots , s_ {j-1 \% k}$ in that order. Notice that we will allow for $j \geq k$. Then a Devil’s algorithm is a sequence of moves $s_ 0,s_ 1,\ldots,s_ {k-1}$ such that given a scrambled Rubik’s Cube, we can specify integer $j$ and then $p_ j$ will give us a solved Rubik’s Cube.
The Devil’s Number is the minimum integer $D$ such that we have a Devil’s Algorithm $s_ 0,s_ 1,\ldots,s_ {d-1}$ of size $D$. We will denote $D_ n$ as the Devil’s Number for $R_ n$.
Now, we also consider that stickers can be rotated and that stickers with the same colors can be swapped to give a valid state. For example, consider perfoming the $2$-move sequence $\texttt{UF}$ $105$ times (the overall effect of this is the identity operation, you can try it).
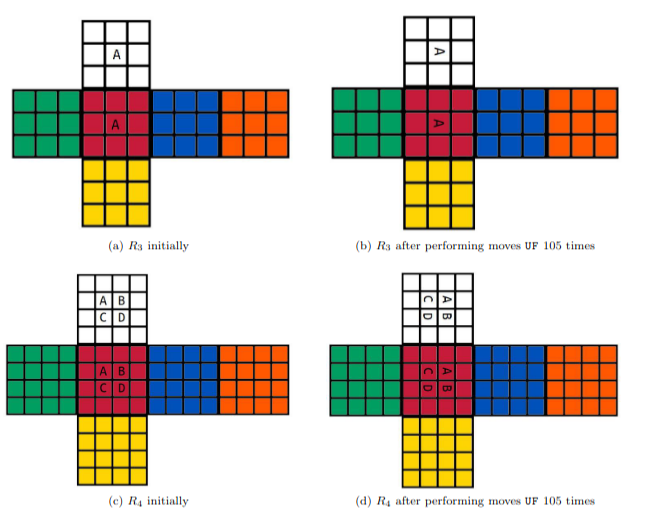
However, I was too lazy to handle the case where stickers are equivalent so my analysis below always assume that all stickers are distinguishable but their rotation is not. So we consider applying $\texttt{UF}$ $105$ times to $R_ 3$ is identity but $R_ 4$ is not.
Now, previous work by Ken F. Fraser and Chris Hardwick has already calculated the number of different states of $R_ n$ where stickers are not distinguishable and they are.
If stickers are not distinguishable, which is our “normal” definition of number of states for $R_ n$ is given by: \(S_ {n,0}= \begin{cases} (7! \cdot 3^6) \cdot (24!)^{\frac{n-2}{2}} \cdot (\frac{24!}{4!})^{\frac{(n-2)^2}{4}},& \text{if } N \text{ is even}\\ (7! \cdot 3^6) \cdot (24!)^{\frac{n-3}{2}} \cdot (\frac{24!}{4!})^{\frac{(n-2)^2-1}{4}} \cdot (12! \cdot 2^{10}) \cdot (24), & \text{if } N \text{ is odd} \end{cases}\) If stickers are distinguishable, which is the definition we will use for the rest of the blog, the number of states for $R_ n$ is given by: \(S_ {n,1}= \begin{cases} (7! \cdot 3^6) \cdot (24!)^{\frac{n-2}{2}} \cdot (\frac{24!}{2})^{\frac{(n-2)^2}{4}},& \text{if } N \text{ is even}\\ (7! \cdot 3^6) \cdot (24!)^{\frac{n-3}{2}} \cdot (\frac{24!}{2})^{\frac{(n-2)^2-1}{4}} \cdot (12! \cdot 2^{10}) \cdot (24), & \text{if } N \text{ is odd} \end{cases}\)
Notice that $S_ {n,0} = S_ {n,1}$ for $n=2,3$. Because all sticker positions on a solved cube is uniquely determined.
Now, in this blog my results are that:
- $D_ 2 = 102061$
- $D_ n \leq 2(\frac{S_ {n,1}}{5354228880}-1)+2331$ for $14 \leq n$
Honestly, the bound on $D_ n$ is very bad because a lower bound is something like $\frac{S_ {n,0}}{5354228880} \leq D_ n$. I believe the actual bound will be something like $D_ n = \frac{S_ {n,0}}{5354228880} +O(1)$. But honestly, the main point of this blog is to show that $D_ 2=102061$. The rest is an afterthought.
Also, our results generally works for all Twisty Puzzles that are not “shape-shifting”. That is we can specify a set of moves $S$ such that we can apply all moves in $S$ no matter which state of we made the Twisty Puzzle into.
Here are some examples of non “shape-shifting” cubes.

Here are some examples of “shape-shifting” cubes.

Previous Works
So, currently the only information I could find about the Devil’s Algorithm for 2x2x2 is this blog which has the bound $102060 \leq D_ 2 \leq 2886840$.
A Hamiltonian circuit for $R_ 2$ has been found in this forum post and gives the upper bound $D_ 2 \leq 2886840$ found in the previous blog.
General Upper Bound Formula
We will now consider a group $G$ of the states of the Rubik’s Cube with the operation is permutation composition and we fixed an arbitrary corner of the Cube. Here, we must force that the stickers are distinguishable for it to be a group. Then if the Rubik’s Cube has $m$ stickers, for example $R_ n$ has $6n^2$ stickers, it is clearly a subgroup of symmetric group on $m$ elements $S_ m$. We fixed a arbitrary corner of the cube because now our group will only contain distinct cubes up to rotation.
We will let $G_ n$ denote the group of the states of $R_ n$ where the bottom right down corner is fixed. So $G_ n$ contains all $R_ n$ that can be made by applying the moves $\{\texttt{U}_ 1,\ldots\texttt{U}_ {n-1},\texttt{U}_ 1’,\ldots\texttt{U}_ {n-1}’,\texttt{L}_ 1,\ldots\texttt{L}_ {n-1},\texttt{L}_ 1’,\ldots\texttt{L}_ {n-1}’,\texttt{F}_ 1,\ldots\texttt{F}_ {n-1},\texttt{F}_ 1’,\ldots\texttt{F}_ {n-1}’\}$.
Some definitions:
- $1_ G$ identity element of group $G$, the “solved” puzzle
- $\text{ord}(G)$, order of group $G$, so we have $\text{ord}(G_ n) = S_ {n,1}$
- $\text{ord}_ G(x)$ order of element $x$ in $G$. We will usually drop the subscript
- $\text{meo}(G) = \max\limits_ {x \in G} \text{ord}(x)$, maximum order of any element in $G$
- $H_ G$ is the underlying graph of $G$ where the vertices of $H_ G$ is the elements in the underlying set of $G$ and there is an undirected edge between elements $a$ and $b$ if we can make a move to go from $a$ to $b$. This is transitive since each move has its inverse. Notably, the moves $\texttt{X}_ i$ and $\texttt{X}_ i’$ are inverses
- $\text{dist}_ G(a,b)$ is the distance in $H_ G$
- $\text{GOD}_ G$ is the diameter of the graph, please convince yourself that this corresponds to God’s Algorithm
Then we will prove that the upper bound of the Devil’s Algorithm is given by $2 (\frac{\text{ord}(G)}{\text{meo}(G)}-1)+\text{GOD}_ G$.
Notice that we just need to find a sequence of moves such that $s_ 0,s_ 1,\ldots,s_ {k-1}$ such that for all $g \in G$, we can pick $j$ such that $p_ j = g^{-1}$.
Let us pick $x \in G$ and consider the left cosets of the subgroup $\braket x$, which we call $C_ x$. $A$ will be the coset containing the element $a$.
We will define a graph $H_ {G,x}$ where vertices are $C_ x$ and there is an edge between $A$ and $B$ if $\text{dist}_ G(a,b)=1$. We will denote $\text{dist}_ {G,x}(A,B)=1$ as the distance between $A$ and $B$ in $H_ {G,x}$.
Now, suppose that $\text{dist}_ {G,x}(A,B)=1$, then for each $a \in A$, there is $b \in B$ such that $\text{dist}_ G(a,b)=1$. This is because by definition there exists $a_ 1 \in A, b_ 1 \in B$ such that $\text{dist}_ G(a,b)=1$ and therefore $b=as$ for some move $s$. Since $a$ and $a_ 1$ are in the same coset, write $a=x^k a_ 1$, and construct $b=x^ka_ 1s = x^kb$.
Now, given that $H_ {G,x}$ is also connected. Therefore, if we find a circuit on $H_ {G,x}$ that visits all vertices and sends state $1_ G$ to state $x^k$ where $\gcd(k,\text{ord}(x)) = 1$, we have found a Devil’s Algorithm which is the length of this circuit.
Suppose that on the first pass where go from state $1_ G$ to state $x^k$, we visit state $a \in A$. Then in the $i$-th pass where we go from state $x^{ik \% \text{ord}(x)}$ to state $x^{(i+1)k \% \text{ord}(x)}$, we will visit state $x^{ik \% \text{ord}(x)} a$. Since $\gcd(k,\text{ord}(x)) = 1$, we will evantually visits all states in $A$ as long as in the first pass we visit some state $a \in A$.
A valid circuit that visits all vertices and send state $1_ G$ to state $1_ G$ is to find any spanning tree in $H_ {G,x}$ and make a Euler tour, which takes $2(\frac{\text{ord}(G)}{\text{ord}(x)}-1)$ moves. Then we need to move to state $x$ (we choose $k=1$), we simply make $\text{dist}_ G(1_ G,x)$ moves. Therefore, we constructed a Devil’s Algorithm using $2(\frac{\text{ord}(G)}{\text{ord}(x)}-1)+\text{dist}_ G(1_ G,x)$ moves.
Using some $x \in G$ with $\text{ord}(x) = \text{meo}(G)$, we have a Devil’s Algorithm using $2(\frac{\text{ord}(G)}{\text{ord}(x)}-1)+\text{dist}_ G(1_ G,x) \leq 2(\frac{\text{ord}(G)}{\text{meo}(G)}-1)+\text{GOD}_ G$.
General Lower Bound Formula
Let $S$ denote the number of states of the Rubik’s Cube when stickers cannot be distinguished. Then the size of the Devil’s Algorithm is at least $\frac{S}{\text{meo}(G)}$.
Suppose we have the sequence of moves $s_ 0,s_ 1,\ldots,s_ {k-1}$ that transforms state $1_ G$ into state $x$. Let $l = \text{ord}(x)$.
Then $p_ k = x$ and $p_ {kl}=x^l = 1_ G$. It is not too hard to see that if $a=b \pmod{kl}$ then $p_ {a}=p_ {b}$. So there are at most $kl$ distinct states.
Therefore if $k < \frac{S}{\text{meo}(G)}$, then $kl < S$. So we all Devil’s Algirothms must have length at least $\frac{S}{\text{meo}(G)}$
Devil’s Number for $R_ 2$
Here, we will prove that $D_ 2 = 102061$.
We know by above that $\text{ord}(G_ 2) = 3674160$ and a brute force yeilds $\text{meo}(G_ 2)=36$ and $GOD_ {G_ 2}=14$.
Therefore, an immediately upper bound is $D_ 2 \leq 204132$.
We can sharpen the bound slightly to $204123$ as we can find an element of order $36$ using the moves $\texttt{U’LULF’}$.
We will attempt to find a Hamiltonian path on $H_ {G,x}$, where $\text{ord}(x)=36$, that sends state $1$ to state $q$. And then we append $\text{dist}_ G(q,x)$ moves to make it a Devil’s Algorithm.
The heuristic is simple. We maintain a valid simple path on $H_ {G,x}$ which initially only contains $1_ G$.
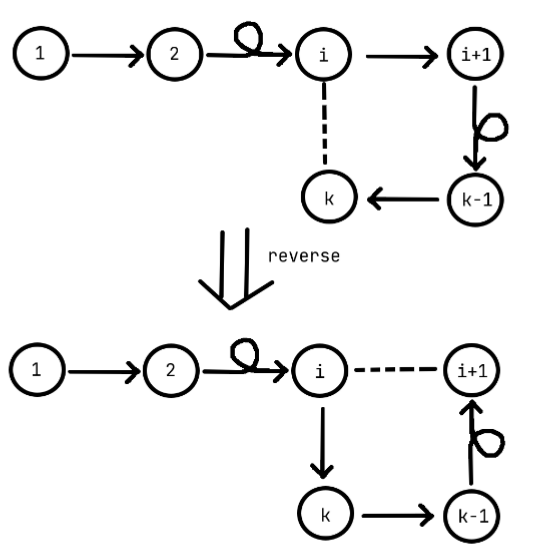
If the current tail of the path has unvisited neighbours, we randomly choose one of them and add them to the path. Otherwise, we use a heuristic that reverses a suffix of the path while leaving it as a valid path. Suppose the path is $q_ 1, q_ 2, \ldots, q_ k$. Since $q_ k$ have no unvisited neighbours, all of its neighbours appears in $q$. Randomly choose one neighbour of $q_ k$ other than $q_ {k-1}$. There are $5$ of them because $deg(q_ k)=6$. Suppose we choose $q_ i$. Then we change the path into $q_ 1, q_ 2, \ldots, q_ i, q_ k, q_ {k-1}, \ldots, q_ {i+1}$. We call this the reverse heuristic.
Surprisingly, by repeating the above procedure for extending the length of the path, we can find a Hamiltonian path in less than $1$ minute. Therefore, we have already obtained a Devil’s algorithm of size at most $\frac{ord(G_ N)}{meo(G_ N)}-1+GOD_ N = 102073$.
To lower the number of moves even further, we must minimize the value of $\text{dist}_ G(q,x)$. A possible idea is to use the reverse heuristic until $q$ is adjacent to $x^k$ for some $\gcd(k,36)=1$. But it turns out that this is impossible.
Lemma 1: $H_ {G_ 2}$ is bipartite
Proof of lemma 1: Consider the stickers of the Rubik’s cube as a permutation of $24$ integers. Then, each move in $M_ N$ is equivalent a permutation of size $24$ that will be composed to the original permutation.
Every permutation that represents a valid move has an odd parity. Consider the move $\texttt{U}$. It is composed of $3$ cycles of size $4$. One cycle on the upper face and $2$ cycles to rotate the stickers on the sides. So the permutation consists of $9$ transpositions and is therefore odd.
The $H_ {G_ 2}$ is bipartite as any state that is represented by an even permutation of stickers is adjacent to those states that are represented by an odd permutation of stickers and vice versa. $\blacksquare$
Lemma 2: any element $x$ with $\text{ord}(x)=36$ has different parity from $1_ G$ in the bipartite graph $H_ {G_ 2}$
Proof of lemma 2: direct DFS on $H_ {G_ 2}$ and bicoloring vertices $\blacksquare$
Lemma 3: $102061 \leq R_ 2$
Proof of Lemma 3: From our general result on lower bound of the Devil’s Number, we know that $\frac{\text{ord}(G_ 2)}{\text{meo}(R_ 2)} =102060 \leq R_ 2$. We will prove that $R_ 2 \neq 102060$.
Suppose there is a sequence of moves $s_ 0,s_ 1,\ldots,s_ {102059}$ that is a Devil’s Algorithm and it transforms state $1_ G$ to state $x$. Then we will only visit at most $102060 \cdot \text{ord}(x)$ different states of $R_ 2$. But $\text{ord}(x) < 36$ by lemma 2, so this sequence of moves cannot be a Devil’s Algorithm.
Therefore, $102061 \leq R_ 2$ $\blacksquare$
The reverse heuristic is able to find a Devil’s algorithm of size $102061$ when we repeatedly apply the heuristic to find a Hamiltonian path where $\text{dist}_ G(q,x^k)=2$ for some $\gcd(k,36)=1$. The full output is available in the github repo here. Please do not copy it to the codebreaker problem.
Since we have found a construction of a Devil’s Algorithm of size $102061$, we conclude that $R_ 2=102061$.
Numerical Upper Bound of the Devil’s Number on $R_ n$
here, we will prove that $D_ n \leq 2(\frac{S_ {n,1}}{5354228880}-1)+2331$ for $14 \leq n$.
To do this, we will first bound $\text{meo}(G_ n)$.
Firstly, if $S_ n$ denotes the symmetric group on $n$ elements, then $\text{ord}_ {S_ n}(x)$ is divisible by $\text{lcm}(1,2,\ldots,n)$. This is because $\text{ord}_ {S_ n}(x)$ is the lowest common multiple of all it’s cycle types.
Then if we have two groups $A$ and $B$ and $\text{ord}_ A(a)$ and $\text{ord}_ B(b)$ is divisble by $d_ A$ and $d_ B$ respectively, then $\text{ord}_ {A \times B}(a,b)$ is divisible by $\text{lcm}(a,b)$.
Let the orbit of a sticker be the set of places where this sticker can go to after some moves. Note that we are not enforcing any constraints that some arbitrary corner of the cube must be fixed here.
There are $2$ distinct types of stickers in a Rubik’s cubes. They are non-center stickers and the center stickers. The center stickers are the stickers on the center of each face, they only exist when $N$ is odd. We classify all the other stickers as non-center stickers.
We define an equivalence class $\sim$ over the stickers such that $a \sim b$ if the orbit of $a$ is equal to the orbit of $b$. For each equivalence class, they either consist of all center stickers or non-center stickers. We consider the state of the Rubik’s cube when only looking at the stickers from a single equivalence class, it forms a group that we call these the non-center group and the center group respectively. The non-center group is a subgroup of $S_ {24}$ and the center group is a subgroup of $S_ {6}$.
Let $a=\lfloor \frac{n^2}{4} \rfloor, b=n \% 2$. $R_ n$ has $a$ non-center groups and $b$ center groups. Therefore, $G_ n$ is a subgroup of the group $S_ {24}^a \times S_ {6}^b$. Then $\text{meo}(G_ n)$ is clearly divisible by $\text{lcm}(1,2,\ldots,24) = 5354228880$.
So $\text{meo}(G_ n)$ is bounded. It makes sense now to consider constructing a state $x$ such that $\text{ord}(x)=5354228880$.
For this, we will only use edge stickers.
Then we will use known algorithms that only swaps two pieces taken from here. Notably:
- $\texttt{R}_ x’\texttt{F}\texttt{L}_ x’\texttt{F}\texttt{F}\texttt{R}_ x\texttt{F}\texttt{R}_ x’\texttt{F}\texttt{F}\texttt{D}\texttt{F}’\texttt{D}\texttt{L}_ x\texttt{D}’\texttt{F}\texttt{D}’\texttt{L}_ x\texttt{F}\texttt{F}\texttt{R}_ x$ (4.1.2, Pure Flips (Single Parity), One dedge flip, Shortest single slice quarter turn algorithms)
- $\texttt{R}_ x’\texttt{U}\texttt{R}\texttt{U}\texttt{R}_ x’\texttt{U}’\texttt{R}’\texttt{U}’\texttt{B}\texttt{B}\texttt{R}_ x’\texttt{B}\texttt{B}\texttt{L}_ x\texttt{U}\texttt{U}\texttt{L}_ x’\texttt{U}\texttt{U}\texttt{R}_ x\texttt{R}_ x$ (8.2.3, Non Dedge-Preserving Last Layer 2-Cycle Cases, In adjacent dedges, Oriented)
Here are examples for $n=4$ and $x=2$:
- $\texttt{R}_ 2’\texttt{F}\texttt{L}_ 2’\texttt{F}\texttt{F}\texttt{R}_ 2\texttt{F}\texttt{R}_ 2’\texttt{F}\texttt{F}\texttt{D}\texttt{F}’\texttt{D}\texttt{L}_ 2\texttt{D}’\texttt{F}\texttt{D}’\texttt{L}_ 2\texttt{F}\texttt{F}\texttt{R}_ 2$

- $\texttt{R}_ 2’\texttt{U}\texttt{R}\texttt{U}\texttt{R}_ 2’\texttt{U}’\texttt{R}’\texttt{U}’\texttt{B}\texttt{B}\texttt{R}_ 2’\texttt{B}\texttt{B}\texttt{L}_ 2\texttt{U}\texttt{U}\texttt{L}_ 2’\texttt{U}\texttt{U}\texttt{R}_ 2\texttt{R}_ 2$

Notice that the center pieces get scrambled. But we don’t care.
The two algorithms both use $21$ our metric.
Using these 2 moves, we can create arbitrary cycles on the edge pieces. We want to create cycles of size $16,9,5,7,11,13,17,19,23$. We can assign these cycles into $6$ different edge orbit groups with the grouping $\{16\},\{9,13\},\{5,17\},\{7,11\},\{19\},\{23\}$. Note that each edge orbit group only has $24$ elements, so the sum of cycle sizes cannot exceed $24$. We need a cube of which is at least as large as $R_ {14}$ so that it will contain at least $6$ different edge orbit groups that we can fit all our cycles into. To put a cycle of size $s$ into the cube state, we will need to swap 2 edge pieces $s-1$ times. So we need $(15+8+4+6+10+12+16+18+22)\cdot 21 = 2331$ moves to put all these cycles into the Rubik’s cube.
We have the result that for $R_ N$, there exists a Devil’s algorithm of size $2 (\frac{\text{ord}(G_ n)}{\text{ord}(x)}-1)+\text{dist}_ {G_ n}(1_ G,x)$ where $x$ is some element in $G_ n$. When $n \geq 14$, we have an element $x$ such that $\text{dist}_ {G_ n}(1_ G,x)=2331$ and $\text{ord}(x)=5354228880$ as shown by our construction above. Therefore, we have an upper bound of $2 (\frac{\text{ord}(G_ N)}{5354228880}-1)+2331$ for the Devil’s number on $R_ N$.