Central-European Olympiad in Informatics (CEOI) 2024 Unofficial Editorial
Covid
Thank to you oolimry for writing the editorial for this problem!
Binary Searching
The most direct method is to binary search until you’re done. This takes an expected $pNlogN$ queries in total. The biggest issue is the $logN$ is big
Bucketing
We define some constant $B$ and split the $N$ elements into groups of $B$. If we query the entire group and it’s negative, then we can ignore the group. Otherwise, we can perform binary search within the group.
If we choose $B$ to the smallest $B$ such that $(1-p)^B \geq 1/2$, this gets 89.19 points
Binary Searching only once
If we find some positive within the group of size $B$, it is inefficient to binary search within the smaller group. Instead, we can have a global list of things which are unknown. Then given some group, we binary search for the first positive within the group.
- Everything before the first positive is negative
- Everything after the first positive is unknown, so we push it back into the global list
My submission using this gets 95.6, which actually mainly blocked by the $p=0.2$ testcase
Engineering the bucket size abit more gets AC. What I did was I changed the value of $B$ to the smallest $B$ such that $(1-p)^B \geq k$ and “ternary-searched” the value of $k$ for each test case. In particular, I found $k=0.50$ for $p = 0.104571$, and $k = 0.57$ for everything else works.
By the way, the below code has some extra stuff for debugging & experimentation, look for the comment for where the main logic begins.
Code
#include <bits/stdc++.h>
using namespace std;
#define sz(x) (int) (x).size()
#define all(x) (x).begin(), (x).end()
#define double long double
typedef pair<int,int> ii;
bool tosubmit = true;
int N, T; double P;
int arr[1005];
vector<int> ans;
vector<int> toquery;
double total = 0;
int query(vector<int> v){
total++;
for(int i : v) toquery[i] = 1;
if(tosubmit){
string S = "Q ";
for(int i = 0;i < sz(toquery);i++){
if(toquery[i]) S += '1';
else S += '0';
}
for(int i : v) toquery[i] = 0;
cout << S << endl;
char res; cin >> res;
if(res == 'P') return true;
else return false;
}
else{
bool toreturn = false;
for(int i = 0;i < N;i++) if(toquery[i] and arr[i]) toreturn = true;
for(int i : v) toquery[i] = 0;
return toreturn;
}
}
void answer(vector<int> v){
assert(sz(v) == N);
if(tosubmit){
string S = "A ";
for(int x : v){
if(x) S += '1';
else S += '0';
}
cout << S << endl;
char res; cin >> res;
}
else{
assert(sz(v) == N);
for(int i = 0;i < N;i++) assert(v[i] == arr[i]);
}
}
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
/// main logic begins here
vector<int> unknown;
void solve(vector<int> v){
if(not query(v)) return;
if(sz(v) == 1){
ans[v[0]] = 1;
return;
}
int low = -1, high = sz(v)-1;
while(low != high-1){
int mid = (low+high)/2;
vector<int> toquery;
for(int i = 0;i <= mid;i++) toquery.push_back(v[i]);
if(query(toquery)) high = mid;
else low = mid;
}
ans[v[high]] = 1;
for(int i = high+1;i < sz(v);i++) unknown.push_back(v[i]);
}
double prob[1005];
signed main(){
if(not tosubmit) freopen("i.txt","r",stdin);
cin >> N >> P >> T;
for(int i = 0;i < N;i++) toquery.push_back(0);
for(int i = 0;i < N;i++) ans.push_back(0);
prob[1] = (1.0-P);
for(int i = 2;i <= N;i++) prob[i] = prob[i-1] * (1.0-P);
int B = 1;
double boundary = 0.57;
if(0.10 < P and P < 0.11) boundary = 0.50;
while(prob[B] > boundary) B++;
for(int t = 0;t < T;t++){
for(int i = 0;i < N;i++) ans[i] = 0;
for(int i = 0;i < N;i++){
int x = (rng()%10000000 < P*10000000.0);
arr[i] = x;
}
unknown.clear();
for(int i = 0;i < N;i++) unknown.push_back(i);
while(sz(unknown) > 0){
vector<int> todo;
while(sz(todo) < B and sz(unknown) > 0){
todo.push_back(unknown.back());
unknown.pop_back();
}
solve(todo);
}
answer(ans);
}
double avg = total;
avg /= (double) T;
cerr << setprecision(10) << avg;
}
Battle
Firstly, let us solve this problem: what is the first time a crash will happen?
We split the crashes into $2$ types:
- A: $(N,E)$, $(N,W)$, $(S,E)$, $(S,W)$
- B: $(N,S)$, $(E,W)$
For convinience, I will talk about group $(S,W)$ in group A and $(E,W)$ in group B.
For group A, if two ships were to collide, then $(x_S-k,y_S) = (x_W,y_W+k)$, for some $k$. It is necessary that $y_S - x_S = y_W - x_W$. Therefore, if we look at the line $y-x=k$ for some $k$, that is the set $(S,W)$ ships that can collide into each other. Then, if we write down all $(S,W)$ ships in a line in order, for example getting the sting $\texttt{WSSSWWWSSWSWSS}$, the pairs of ships that are a candidate for being the first crash are any adjacent ships of the form $\texttt{WS}$. In our above example, it would be pairs (by index) $(1,2)$, $(7,8)$, $(10,11)$, $(12,13)$.
For group B, it is similar. Suppose we take the line $x=k$ and write down all $(E,W)$ ships in a line in order, we will try all adjacent $(E,W)$ pairs.
Now, we have solved the subproblem of figuring out when the first crash will happen.
To solve the entire problem, we have to find the first crash, figure out which ships are involved, remove them and recalculate the first crash again.
Notice that our algorithm for finding when the first crash will happen can be made to handle arbitrary deletions of ships if we use a set or priority queue for example, so just do that. Implementation is honestly not that bad if you plan it well by abstracting all cases into a single class. Refer to the implementation.
I’m not sure whether a set would pass the time limit as the complexity is like $3 N \log N$.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
ii arr[200005];
char c[200005];
bool has[200005];
priority_queue<iii,vector<iii>,greater<iii> > pq;
struct dat{
vector<int> idx;
ii cmp1; //those with same cmp1 are same
ii cmp2; //tiebreak by cmp2
char ca,cb; //needs a and b to be adjacent to each other
//cursed...
int nxt[200005];
int prv[200005];
int dot(ii a,ii b){
return a.fi*b.fi + a.se*b.se;
}
bool can(int i,int j){
return dot(arr[i],cmp1)==dot(arr[j],cmp1) && c[i]==ca && c[j]==cb;
}
int dist(int i,int j){
return abs(arr[i].fi-arr[j].fi)+abs(arr[i].se-arr[j].se);
}
void init(){
memset(nxt,-1,sizeof(nxt));
memset(prv,-1,sizeof(prv));
if (idx.empty()) return;
sort(all(idx),[this](int i,int j){
ii a=arr[i],b=arr[j];
if (dot(a,cmp1)!=dot(b,cmp1)) return dot(a,cmp1)<dot(b,cmp1);
else return dot(a,cmp2)<dot(b,cmp2);
});
rep(x,0,sz(idx)-1){
nxt[idx[x]]=idx[x+1];
prv[idx[x+1]]=idx[x];
if (can(idx[x],idx[x+1])) pq.push({dist(idx[x],idx[x+1]),idx[x],idx[x+1]});
}
}
void rem(int i){
int pp=prv[i],nn=nxt[i];
if (pp!=-1) nxt[pp]=nn;
if (nn!=-1) prv[nn]=pp;
if (pp!=-1 && nn!=-1 && can(pp,nn)) pq.push({dist(pp,nn),pp,nn});
}
} d[6];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n;
rep(x,1,n+1) cin>>arr[x].fi>>arr[x].se>>c[x];
//NE, NW, SE, SW, NS, EW
d[0].cmp1={1,-1},d[0].cmp2={1,0},d[0].ca='E',d[0].cb='N';
d[1].cmp1={1,1},d[1].cmp2={1,0},d[1].ca='N',d[1].cb='W';
d[2].cmp1={1,1},d[2].cmp2={1,0},d[2].ca='E',d[2].cb='S';
d[3].cmp1={1,-1},d[3].cmp2={1,0},d[3].ca='S',d[3].cb='W';
d[4].cmp1={1,0},d[4].cmp2={0,1},d[4].ca='S',d[4].cb='N';
d[5].cmp1={0,1},d[5].cmp2={1,0},d[5].ca='E',d[5].cb='W';
map<char,vector<int> > M={
{'N',{0,1,4}},
{'S',{2,3,4}},
{'E',{0,2,5}},
{'W',{1,3,5}}
};
rep(x,1,n+1) for (auto it:M[c[x]]) d[it].idx.pub(x);
rep(x,0,6) d[x].init();
while (!pq.empty()){
int w,a,b; tie(w,a,b)=pq.top(); pq.pop();
if (has[a] || has[b]) continue;
set<int> s={a,b};
while (!pq.empty() && get<0>(pq.top())==w){
tie(w,a,b)=pq.top(); pq.pop();
if (!has[a] && !has[b]) s.insert(a),s.insert(b);
}
for (auto x:s){
has[x]=true;
for (auto it:M[c[x]]) d[it].rem(x);
}
}
rep(x,1,n+1) if (!has[x]) cout<<x<<endl;
}
Editor
This in editorial, the points will be labelled from $(i,0)$ to $(i,l_i)$, unlike the statement using $(i,1)$ to $(i,l_i+1)$.
We will call $(i,0)$ and $(i,l_i)$ special. Because if we do not use any special points, then the distance between $2$ points is pretty much their manhattan distance (using pretty much because it is sometimes not possible).
Firstly, let us consider when we can go from $s$ to $e$ using manhattan distance of keystroke without touching any special. Consider the array $l=[10,2,10]$, $s=(1,6)$ and $e=(3,9)$. The manhattan distance between these $2$ points is $5$, but it is not possible to use only $5$ moves if we don’t use special points since we are forced to take a detour to $(2,1)$. But it is not hard to see that if between $s_x$ and $e_x$, if $l_i \geq \min(s_y,e_y)$, then it is possible to travel through them via their manhattan distance.
Now, that is the only case where we go from $s$ to $e$ without touching any special points. Otherwise, we will assume that we will pass through special points. And even more, we will only care with connecting:
- $s$ to special points
- special points to special points
- special points to $e$
Let us break special points into $2$ more types:
- head points: $(i,0)$
- tail points: $(i,l_i)$
Other than travelling by Manhattan distance, there are $2$ special moves that we need to care about:
- special move A: moving from head to tail and vice versa: $(i,l_i) \leftrightarrow (i+1,0)$
- special move B: moving from arbitrary point to a tail point: $(i,Y) \to (i\pm 1,l_{i\pm 1})$, where $Y \geq l_{i \pm 1}$.
We will demonstrate how to build a graph with $O(n)$ vertices and edges so that we can run Dijkstra on it.
First, we will build these (trivial) edges:
- Between adjacent head points, that is $(i,0) \leftrightarrow (i+1,0)$, add an undirected edge of weight $1$.
- Between all $n$ pairs of head and tail points, that is $(i,0) \leftrightarrow (i,l_i)$, add an undirected edge of weight $l_i$.
- Special move A, that is $(i,l_i) \leftrightarrow (i+1,0)$, add an undirected edge of weight $1$.
- Add directed edges $s \to (s_x,0)$ and $(e_x,0) \to e$ with weights $s_y$ and $e_y$ respectively.
Now, we will make a helpful observation: in a optimal path, we should use special move A at most twice, at most one time from tail to head point, and then at most one time from head to tail point.
To prove that the above is true, consider doing any other consecutive pair of special move, it is useless because travelling using normal moves through head points is much faster.
Therefore, an optimal strategy is one of the following:
- go from $s$ to one head point, use the head points as a “highway”, then go to $e$ from another head point
- go from $s$ to $e$ without touching head points
Consider adding edges from $s$ to all tail points and likewise from tail points to $e$. The optimal strategy to go from $s$ to $(i,l_i)$ is to press up/down until we go to that row and then press right. Similarly, our strategy to go from $(i,l_i)$ to $e$ is to press up/down until we go that row and then press left/right.
So, we do not need to care about adding edges between tail points and other tail points. This is because the strategy for going between tail points and tail points is the exact same as our strategy to go from the source/sink to tail points. Because of our more global optimal strategy to immediately use special move A to go to a head point after we have reached a tail points, these moves are redundant.
The cost to go from $s$ to $(i,l_i)$ is $\lvert s_x - i \rvert + l_i - \min(s_y, \min\limits_{i \leq x \leq s} l_x)$ and the cost to go from $(i,l_i)$ to $e$ is $\lvert t_x - i \rvert + \lvert t_y - \min\limits_{i \leq x \leq s} l_x \rvert$. So we will add these edges to our graph, which completes our graph modelling.
Previous modeeling for tail points before I realized they were useless
Now, we come to the non-trivial part, adding edges between tail points and from tail points to $s$ and $e$.
Note that we only need to consider the distance between tail points if we are not allowed to touch any head points, as the edges added above will handle that. Therefore, we only need to care about Manhattan distance and special move B.
Now, what is the distance between two tail points under our conditions? The strategy for us is to press up/down until we hit our desired row and then hit right. Proof is left as an exercise.
So the distance from $(i,l_i) \to (j,l_j)$ is $\lvert i-j \rvert + l_j - \min\limits_{i \leq x \leq j} l_x$. The situation is quite similar when considering $s$ to tail points and tail points to $e$.
We will now consider how to cut these $O(n^2)$ edges into $O(n)$ edges.
Firstly, suppose that $\min\limits_{i < x < j} l_x \leq \min(l_i,l_j)$, then let $m$ be the index of the minimal element in $(i,j)$, then the edge $i \to j$ is represented by the edges $i \to m \to j$. Therefore, if we let $L_i$ and $R_i$ the first index $k$ to the left and right respectively such that $l_k \leq l_i$, it only makes sense to connect $(i,l_i)$ with $(j,l_j)$ if $j \in [L_i,R_i]$.
We will connect edges $(i,l_i) \to (L_i,l_{L_i})$ and $(i,l_i) \to (R_i,l_{R_i})$ which is still under our budget for $O(n)$ edges.
Then, notice that for $j \in (L_i,R_i)$, the distance of $(i,l_i) \to (j,l_i)$ is $\lvert i-j \rvert + l_j - l_i$. Suppose that $L_i<a<b<i$ and $l_a>l_b>l_i$. Then the edge $i \to a$ is represented by the edges $i \to b \to a$.
If we maintain a max stack, the edges $i \to j$ that we need to add in the above case are just the elements that we pop from the max stack. This is $O(n)$, so the number of edges we add are $O(n)$ in total.
There are some additional details when considering adding edges from $s$ to tail points and tail points to $e$, but it is not too hard to figure them them. Or you can just look at the code.
Total complexity is $O(n \log n)$ cause of Dijkstra.
Open problem: In this problem, we only have a single pair of start and end points. What if we have $O(q)$ pairs of start and end points. Is it possible to solve this in linearithmic time?
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
ii s,t;
int arr[1000005];
vector<ii> al[2000005];
int w[2000005];
priority_queue<ii,vector<ii>,greater<ii> > pq;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n;
cin>>s.fi>>s.se;
cin>>t.fi>>t.se;
s.se--,t.se--; //silly
rep(x,1,n+1) cin>>arr[x];
//0 is the source, 1 is the sink
//2*x is first
//2*x+1 is last
rep(x,1,n+1){
//between first and last slow (quite stupid cause of next, but whatever)
al[2*x].pub({2*x+1,arr[x]});
al[2*x+1].pub({2*x,arr[x]});
//between firsts and last but faster
if (x!=1) al[2*x].pub({2*(x-1)+1,1});
if (x!=n) al[2*x+1].pub({2*(x+1),1});
//between firsts
if (x!=1) al[2*x].pub({2*(x-1),1});
if (x!=n) al[2*x].pub({2*(x+1),1});
//between firsts and source/sink
al[0].pub({2*x,abs(x-s.fi)+s.se});
al[2*x].pub({1,abs(x-t.fi)+t.se});
}
for (auto [l,r]:vector<ii>{ {s.fi+1,1},{s.fi,n+1} }){ //source to last
int mn=s.se;
rep(x,l,r){
mn=min(mn,arr[x]);
al[0].pub({2*x+1,abs(s.fi-x)+arr[x]-mn});
}
}
for (auto [l,r]:vector<ii>{ {t.fi+1,1},{t.fi,n+1} }){ //sink to last
int curr=2e9;
rep(x,l,r) if (curr>arr[x]){
curr=arr[x];
al[2*x+1].pub({1,abs(t.fi-x)+abs(curr-t.se)});
}
}
memset(w,1,sizeof(w));
w[0]=0;
pq.push({w[0],0});
while (!pq.empty()){
int u,v; tie(v,u)=pq.top(); pq.pop();
if (w[u]!=v) continue;
for (auto [u2,ww]:al[u]) if (w[u2]>v+ww){
w[u2]=v+ww;
pq.push({w[u2],u2});
}
}
bool ok=true;
rep(x,min(s.fi,t.fi),max(s.fi,t.fi)+1) if (arr[x]<min(s.se,t.se)) ok=false;
if (ok) w[1]=min(w[1],abs(s.fi-t.fi)+abs(s.se-t.se));
cout<<w[1]<<endl;
}
Toy
The main idea here is instead of storing the positions of the horizontal and center piece as our state, we will instead store the position of their intersection.
For every move we make, the intersection either does not move or only moves to an adjacent cell.
Suppose that we have the intersection on cell $(x,y)$. When are we allowed to move it to cell $(x \pm 1,y)$? Obviously a necessary condition is that cell $(x\pm 1,y)$ has to be empty. If cell $(x\pm 1,y)$ is empty, we can surely slide the vertical piece to touch $(x \pm 1,y)$. Now we just need to figure if we can slide the vertical piece to column $x+1$.
Define $\text{left}_ {x,y}$ and $\text{right}_ {x,y}$ to be the number of spaces to the left and right of cell $(x,y)$ respectively. For the piece to move from $(x,y)$ to $(x\pm 1,y)$, we must have $\min(\text{left}_ {x,y}, \text{left}_ {x\pm 1,y}) + \min(\text{right}_ {x,y}, \text{right}_ {x\pm 1,y}) \geq K+1$.
Similarly, define arrays $\text{up}$ and $\text{down}$. Then for the piece to move from $(x,y)$ to $(x,y\pm 1)$, we must have $\min(\text{up}_ {x,y}, \text{up}_ {x,y\pm 1}) + \min(\text{down}_ {x,y}, \text{down}_ {x,y\pm 1}) \geq K+1$.
From here, just doing a dfs is enough.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n,m,a,b;
int X1,Y1,X2,Y2;
string s[1505];
bool vis[1505][1505];
int U[1505][1505];
int D[1505][1505];
int L[1505][1505];
int R[1505][1505];
void dfs(int i,int j){
if (vis[i][j]) return;
vis[i][j]=true;
if (i!=1 && min(L[i-1][j],L[i][j])+min(R[i-1][j],R[i][j])>=a+1) dfs(i-1,j);
if (i!=n && min(L[i+1][j],L[i][j])+min(R[i+1][j],R[i][j])>=a+1) dfs(i+1,j);
if (j!=1 && min(U[i][j-1],U[i][j])+min(D[i][j-1],D[i][j])>=b+1) dfs(i,j-1);
if (j!=m && min(U[i][j+1],U[i][j])+min(D[i][j+1],D[i][j])>=b+1) dfs(i,j+1);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>m>>a>>b;
swap(n,m); //wtf???
cin>>X1>>Y1>>X2>>Y2;
rep(x,1,n+1) cin>>s[x],s[x]="$"+s[x];
memset(L,-2,sizeof(L));
memset(R,-2,sizeof(R));
memset(U,-2,sizeof(U));
memset(D,-2,sizeof(D));
rep(x,1,n+1) rep(y,1,m+1) if (s[x][y]!='X'){
U[x][y]=1+max(U[x-1][y],0LL);
L[x][y]=1+max(L[x][y-1],0LL);
}
rep(x,n+1,1) rep(y,m+1,1) if (s[x][y]!='X'){
D[x][y]=1+max(D[x+1][y],0LL);
R[x][y]=1+max(R[x][y+1],0LL);
}
dfs(Y1+1,X2+1);
bool win=false;
rep(x,1,n+1) rep(y,1,m+1) if (s[x][y]=='*' && vis[x][y]) win=true;
if (win) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
Stations
Thanks to oolimry for writing the editorial (before I found a cleaner solution :P)
Subtask 4 + Full solution
(Probably there is a simpler way for subtask 4, but let’s discuss a way that transitions to the full solution)
For the full solution, we consider all paths $(a,b)$ that pass through the centroid of the tree $c$. For all other paths that do not pass through the centroid, we can recurse seperately.
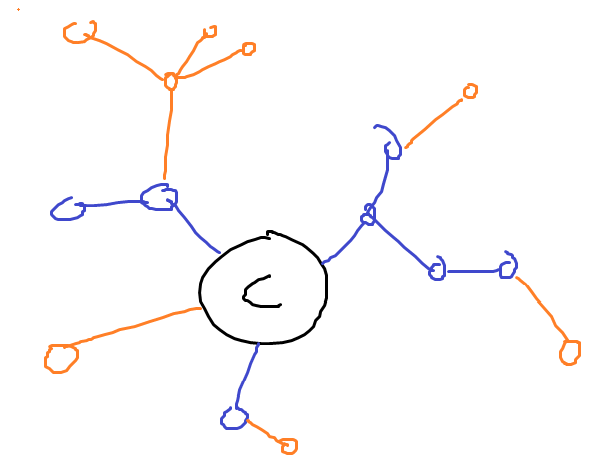
Definitions first:
- $p(u)$ is the parent of node $u$
- $w(u)$ is the weight of the edge from $u$ to $p(u)$
- $d(u,v)$ is the distance between $u$ and $v$
Firstly we root the tree the centroid and find the distances to all nodes. Let’s call the nodes less than distance $K$ of the centroid close (blue) and everything else far (orange).
For every path $(a,b)$, we split it into two halves - the towards centroid half and the away from centroid half. For each node, we count the number of times it stops there seperately for each half.
Towards Centroid
For every node far node $f$, let’s say we start with a full tank, let $g$ be the node that we will need to replenish fuel at. On a new tree (call it the jump-tree), we say $g$ is the jump-parent of $f$. Each close node will not have a jump-parent
Let $to(u)$ be the number of nodes in the subtree of $u$ such that if we start there, we will need to replenish at $u$. We can compute $to(u)$ from the $to$ of all children of $v$ on the jump-tree.
Hence, $to(u)$ gives us the number of good starting points. We can multiply this by the number of good ending points which is the number of points on the other side of the centroid.
(Implementation wise, I believe we can consider the centroid itself as towards centroid, and ignore the centroid for the away from centroid half).
Away from centroid
Subtask 4 $(K \leq 10)$
Suppose we start at the centroid with $k$ fuel remaining. We can simulate the process out towards all nodes to see if we were to try to travel to all nodes, which nodes we would need to refuel at.
We can precompute for each starting point, how many starting points will reach the centroid with $k$ fuel left. Then for each node $u$, we try every $k$. If the value of $k$ requires us to refuel at $p(u)$ before reaching $u$, then all nodes in $u$’s subtree is a good endpoint, and so we multiply that with the start points.
Full solution
Again, we precompute for each starting point, how many starting points will reach the centroid with $k$ fuel left.
Let $count(u)$ be the number of starting points such that we must refuel at $p(u)$ before travelling to $u$.
For all close nodes, we can compute $count(u)$ directly from its distance to the centroid. Now let’s look at a far node, if we must refill at $p(u)$, let’s consider where would be our previous refill position $q$.
We need $d(q,p(u)) \leq K$ and $d(q,u) > K$. $count(u)$ is the sum of $count(q)$ for all valid $q$. Notice that the range of $q$ forms a contiguous range of nodes on the path from $u$ to the centroid. This can be achieved by maintaining a fenwick tree of the values of $count$ for all parents when doing dfs on the tree.
Note that for implementation, it might be easier to imagine add a car with fuel tank $x$ on a path of length $k-x$ above the root instead.
alternate (horrible) solution before we found a better solution
Let $refill(u,k)$ be the number of refills needed to reach node $u$ given the tank initially has $k$ fuel when at the centroid. We can see that
- $refill(u,K) = refill(u,0)+1$
- $refill(u,k) \leq refill(u,k-1)$
This means that for every node $u$, there exists a value of $k’$ such that $refill(u,k’-1) = refill(u,k’)+1$. Let this value be $k’(u)$. In other words, if we increase $k$ from $0$, $k’$ is the value which the number of refills decreases by $1$
Recall that we are trying to determine for which values of $k$, will it be neccessary to refill at $p(u)$ before travelling to $u$. This requires:
\[refill(p(u),k) + 1 = refill(u,k)\]It takes one more refill to reach $u$ than it does $p(u)$, which implies a refill is performed at $p(u)$.
Let’s consider two cases:
Case 1: $refill(p(u),0) = refill(u,0)$
In this case, the range of good $k$ is $[k’(p(u)), k’(u)-1]$
Case 2: $refill(p(u),0)+1 = refill(u,0)$
In this case there are two good ranges of $k$:
- Before $refill(u,0)$ decreases by 1: so $[0, k’(u)-1]$
- After $refill(p(u),0)$ decreases by 1: $[k’(p(u)),K]$
Now, all that remains is a method to find $k’(u)$ for all $u$. We binary search some value of $k$, and determine $refill(u,k)$.
To determine $refill(u,k)$ quickly, we can binary lift to the first parent $q$ where $refill(q,k) < refill(p(u),k)$, which means we had to refill at $q$. Then we check if the distance of $q$ to $u$ is larger than $K$ or not.
Total complexity is $O(n \log^2 n)$.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
struct FEN{
int fen[140005];
void update(int i,int k){
while (i<140005){
fen[i]+=k;
i+=i&-i;
}
}
void set(int i,int k){
update(i,k-query(ii(i,i)));
}
int query(int i){
int res=0;
while (i){
res+=fen[i];
i-=i&-i;
}
return res;
}
int query(ii r){
return query(r.se)-query(r.fi-1);
}
void clear(int n){
rep(x,1,n+1) fen[x]=0;
}
} fen;
int n,k;
vector<ii> al[70005];
bool has[70005];
int ss[70005];
int ans[70005];
void dfs_ss(int i,int p){
ss[i]=1;
for (auto [it,w]:al[i]) if (!has[it] && it!=p){
dfs_ss(it,i);
ss[i]+=ss[it];
}
}
vector<ii> stk;
int tmp[70005];
void up(int i,int p,int num,vector<int> &v){
tmp[i]=1;
for (auto [it,w]:al[i]) if (!has[it] && it!=p){
stk.pub({stk.back().fi+w,it});
up(it,i,num,v);
stk.pob();
}
ans[i]+=(tmp[i]-1)*num;
if (stk.back().fi>k){
auto idx=lb(all(stk),ii(stk.back().fi-k,-1))-stk.begin();
tmp[stk[idx].se]+=tmp[i];
}
else{
rep(x,0,tmp[i]) v.pub(k-stk.back().fi);
}
}
vector<int> uni;
ii get(int l,int r){
//everyone between l and r
return {
lb(all(uni),l)-uni.begin(),
ub(all(uni),r)-uni.begin()-1
};
}
void down(int i,int p,int d){
for (auto [it,w]:al[i]) if (!has[it] && it!=p){
//d is our current position
//d+w is our next position
//anything [d-k,d-k+w-1] must be cleared
int val=fen.query(get(d-k,d-k+w-1));
ans[i]+=val*ss[it];
fen.set(sz(uni),val);
uni.pub(d);
down(it,i,d+w);
uni.pob();
}
}
void centroid(int i){
dfs_ss(i,-1);
int curr=i,currp=-1;
while (true){
bool b=true;
for (auto [it,w]:al[curr]) if (!has[it] && it!=currp && ss[it]>=(ss[i]+1)/2){
currp=curr;
curr=it;
b=false;
break;
}
if (b) break;
}
uni={-1,0,k};
vector<vector<int> > sub; //list of remaining costs under each subtree
dfs_ss(curr,-1);
for (auto [it,w]:al[curr]) if (!has[it]){
stk=;
vector<int> v;
up(it,curr,ss[curr]-ss[it],v);
sub.pub(v);
for (auto it:v) uni.pub(it);
}
sort(all(uni));
fen.clear(sz(uni));
for (auto v:sub) for (auto it:v) fen.update(lb(all(uni),it)-uni.begin(),1);
int idx=0;
for (auto [it,w]:al[curr]) if (!has[it]){
for (auto it:sub[idx]) fen.update(lb(all(uni),it)-uni.begin(),-1);
//add the root
//everyone who is [0,w-1] should be added?
//consider the root
int val=fen.query(get(0,w-1));
ans[curr]+=val*ss[it];
fen.set(sz(uni),val+1);
uni.pub(k);
down(it,curr,k+w);
uni.pob();
for (auto it:sub[idx]) fen.update(lb(all(uni),it)-uni.begin(),1);
idx++;
}
has[curr]=true;
for (auto [it,w]:al[curr]) if (!has[it]) centroid(it);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>k;
rep(x,1,n){
int a,b,c; cin>>a>>b>>c;
al[a].pub({b,c});
al[b].pub({a,c});
}
centroid(0);
rep(x,0,n) cout<<ans[x]<<endl;
}
Sprinklers
Firstly, since the problem is asking for the minimum power $K$ neccessary, we should binary search the answer.
Firstly, note that assigning sprinklers to floewrs is not trivial. We cannot do it greedily. For example, the greedy of considering the sprinklers left to right, then point the sprinkler left if there is a flower to the left, otherwise point it to the right. This is because of a case like $s=[2,4]$ and $f=[1,3,5]$. Where the assignment has to be $\texttt{RL}$.
So consider the following DP state, $dp_x$ is the maximum $y$ such that we cover all flowers in $[1,y]$ and only flowers in $[1,y]$ using the sprinklers $[1,x]$. Because of our DP definition, it is possible (and necessary) for us to consider cases of $dp_x \to dp_{x+2}$, $dp_x \to dp_{x+3}$, etc.
Consider adding a suffix of directions to some dp state, for example $\texttt{RRLRLL}$. If the suffix contains more than one $\texttt{L}$, we can split up the transition into $2$ seperate transitions, for example $\texttt{RRLRLL} \to \texttt{RRL} + \texttt{RLL}$. Suppose adding $\texttt{RRL}$ does not cover a prefix of flowers, then it is impossible that adding $ \texttt{RLL}$ does not covre that uncovered flower in the prefix.
So, the possible transitions we can make are curently:
- $\texttt{R}$
- $\texttt{L}$
- $\texttt{RL}$
- $\texttt{RRL}$
- $\texttt{RRRL}$
- $\ldots$
Actually, we only need to care about $\texttt{R}$, $\texttt{L}$ and $\texttt{RL}$. Consider $\texttt{RRRL}$ for example, adding the suffix $\texttt{LLRL}$ will cover the exact same set of flowers, if the transition $\texttt{R}$ cannot be made.
Therefore, we have a linear DP by only consider the transitions $\texttt{R}$, $\texttt{L}$ and $\texttt{RL}$.
The total complexity $O(n \log \text{MAX})$ after considering the binary search
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n,m;
int arr[100005];
int brr[100005];
#define si pair<int,string> //so we can store the backtracking
si pp[100005];
int dp[100005];
int get_idx(int i){
return ub(brr,brr+m+1,i)-1-brr;
}
bool can(int k){
rep(x,1,n+1){
if (brr[dp[x-1]+1]<arr[x]-k) return false;
if (brr[dp[x-1]+1]>=arr[x]){
dp[x]=get_idx(arr[x]+k);
pp[x]={x-1,"R"};
}
else{
dp[x]=get_idx(arr[x]);
pp[x]={x-1,"L"};
}
if (x>=2 && brr[dp[x-2]+1]>=arr[x]-k && dp[x]<get_idx(arr[x-1]+k)){
dp[x]=get_idx(arr[x-1]+k);
pp[x]={x-2,"LR"};
}
}
return dp[n]==m;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>m;
rep(x,1,n+1) cin>>arr[x];
rep(x,1,m+1) cin>>brr[x];
brr[m+1]=2e9+100000;
int lo=-1,hi=1e9+100,mi;
while (hi-lo>1){
mi=hi+lo>>1;
if (can(mi)) hi=mi;
else lo=mi;
}
if (hi==1e9+100){
cout<<"-1"<<endl;
return 0;
}
can(hi);
cout<<hi<<endl;
int curr=n;
string ans;
while (curr){
ans+=pp[curr].se;
curr=pp[curr].fi;
}
reverse(all(ans));
cout<<ans<<endl;
}