Croatian Olympiad in Informatics 2024
I virtualed the contest at the latest possible time. Was quite late, so I probably quit at around the halfway mark because P3 seemed impossible. I solved it the next day
The third and forth problems were nice, I still find P3 to be super magic, congrats to Agnus for this amazing problem.
CERN
The necessary and sufficient condition to clear all elements of an array is that the array is even and no element occurs more than half the time.
Let $len=r-l+1$.
If $len$ is even:
- If there are 2 elements which both occurs $\frac{len}{2}$ times, then the answer is $0$
- Else if there is 1 element which occurs $\geq \frac{len}{2}$ times, then the answer is $1$
- Else the answer is the number of elements which occurs at least $2$ times
If $len$ is odd:
- If there is 1 element which occurs $\geq \frac{len+1}{2}$ times, then the answer is $1$
- Else the answer is the number of elements which occur at least $1$ time
We split this problem into 2 parts:
- Subproblem A: checking whether there is a element that occurs more than half the time
- Subproblem B: counting the number of elements which occur at least $1$/$2$ times in a range
For subproblem A, we will adapt the Boyer-Moore Algorithm to fit within a segment tree. This is sufficient for the odd case, but for the even case it will not work if the element occurs exactly $\frac{len}{2}$ times. To fix this, split the array into sizes $1$ and $len-1$. Then if an element occurs exactly $\frac{len}{2}$ times, it will be a strict majority in one of the parts. Furthermore, for the first case of $2$ elements occurring both $\frac{len}{2}$ times, they will be the strict majority element on one of the sides.
For subproblem B, perform a line sweep and use a fenwick tree to store the position of the $1$st or $2$nd occurance of each element, then number of $1$st or $2$nd occurance becomes a range query.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
struct dat{
int val;
int num;
};
dat merge(dat a,dat b){
if (a.num<b.num) swap(a,b);
if (a.val!=b.val) a.num-=b.num;
else a.num+=b.num;
return a;
}
struct FEN{
int fen[500005];
void update(int i,int j){
while (i<500005){
fen[i]+=j;
i+=i&-i;
}
}
int query(int i){
int res=0;
while (i){
res+=fen[i];
i-=i&-i;
}
return res;
}
} f1,f2;
int n,q;
int arr[500005];
vector<int> pos[500005];
int occ[500005];
int occ2[500005];
struct node{
int s,e,m;
dat val;
node *l,*r;
node (int _s,int _e){
s=_s,e=_e,m=s+e>>1;
if (s!=e){
l=new node(s,m);
r=new node(m+1,e);
val=merge(l->val,r->val);
}
else{
val={arr[s],1};
}
}
dat query(int i,int j){
if (s==i && e==j) return val;
else if (j<=m) return l->query(i,j);
else if (m<i) return r->query(i,j);
else return merge(l->query(i,m),r->query(m+1,j));
}
} *root;
int ans[500005];
vector<ii> Q[500005];
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>q;
rep(x,1,n+1) cin>>arr[x];
rep(x,1,n+1) pos[arr[x]].pub(x);
root=new node(1,n);
memset(ans,-1,sizeof(ans));
rep(x,0,q){
int a,b; cin>>a>>b;
Q[a].pub({b,x});
vector<int> V={arr[a],root->query(a+1,b).val};
set<int> S;
for (auto v:V) if ((ub(all(pos[v]),b) - lb(all(pos[v]),a))*2 >= b-a+1) S.insert(v);
if (sz(S)==1) ans[x]=1;
if (sz(S)==2) ans[x]=0;
}
memset(occ,-1,sizeof(occ));
memset(occ2,-1,sizeof(occ2));
rep(x,n+1,1){
f1.update(x,1);
if (occ[arr[x]]!=-1) f1.update(occ[arr[x]],-1),f2.update(occ[arr[x]],1);
if (occ2[arr[x]]!=-1) f2.update(occ2[arr[x]],-1);
occ2[arr[x]]=occ[arr[x]];
occ[arr[x]]=x;
for (auto [r,idx]:Q[x]){
int val=((r-x)%2==1)?f2.query(r):f1.query(r);
if (ans[idx]==-1) ans[idx]=val;
}
}
rep(x,0,q) cout<<ans[x]<<endl;
}
Koreografijia
In usual fashion of interactive problems, we will use binary search.
Suppose we know the ordering of elements in $[1,r)$, we will figure out where to insert element $r$ into the sorted order of the previous elements.
How can we determine the relative ordering of $a_l$ and $a_r$? If we query both $[l+1,r]$ and $[l,r]$, the result will be the parity of the number of elements in $[l+1,r]$ that are smaller than $a_l$. However, by our assumption of knowing the ordering of elements in $[1,r)$, we already know how many elements in $[l+1,r)$ are smaller than $a_l$, which allows us to determine the relative ordering of $a_l$ and $a_r$. Therefore, we can perform the binary search, where $1$ comparison takes $2$ queries.
Total queries: $2 n \log n$.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n=1000;
int arr[1005];
int query(int i,int j){
cout<<"? "<<i<<" "<<j<<endl;
int res; cin>>res;
return res;
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
//cin>>n;
arr[1]=1;
rep(x,2,n+1){
vector<int> idx;
rep(y,1,x) idx.pub(y);
sort(all(idx),[](int i,int j){
return arr[i]<arr[j];
});
int lo=0,hi=x,mi;
while (hi-lo>1){
mi=hi+lo>>1;
int pos=idx[mi-1];
int g=query(pos,x)^query(pos+1,x);
rep(y,pos+1,x) if (arr[pos]>arr[y]) g^=1;
if (g==1) hi=mi;
else lo=mi;
}
rep(y,1,x) if (arr[y]>=hi) arr[y]++;
arr[x]=hi;
}
cout<<"!"<<endl;
rep(x,1,n+1) cout<<arr[x]<<" "; cout<<endl;
}
Ministarstvo
If a vertex has outdegree of $n-1$, then it is impossible, since it can reach all vertices.
For $k=3$, this is my construction:
Let $A$ be the vertices that takes in a edge from vertex $1$ and $B$ be the vertices that gives out an edge to vertex $1$.
We will color edges according to the following scheme.
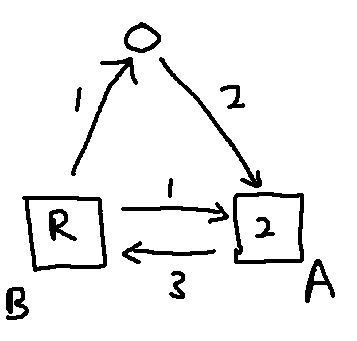
Inside block $B$, R denotes that the edges there are colored recursively:
- Case 1: There is a vertex of degree $m-1$ in that subgraph (of size $m$), then color all edges of $R$ in color $2$
- Case 2: Otherwise, color all edges of $R$ using our algorithm to ensure that it satisfies the condition in the statement.
It is clear that vertex $1$ and all vertices in $A$ satisfy the condition.
Now, to prove that all vertices in $B$ satisfy the condition we split into cases:
- Case 1: Let $x$ be vertex of degree $m-1$ in the subgraph of size $m$. If $x$ uses color $2$ or $3$, it will not reach any vertices in $A$. If $x$ uses color $1$, it can only reach those vertices that it is directly connected to. So it cannot reach all vertices, or it will contradict our assumption that $x$ has outdegree less than $n-1$ in the original graph. Otherwise, for all vertices that are not $x$ in $B$, it needs to pass through $A$ to get to $x$, but going from $B$ to $A$ and back uses at least $2$ colors.
- Case 2: By our assumption of construction of $B$, for each vertex in $x$, there exists a vertex $y$ that $x$ cannot reach by only traversing vertices in $B$. So, it is forced to pass through $A$ to reach $y$, but going from $B$ to $A$ and back uses at least $2$ colors.
To prove that $k=2$ is impossible, see https://math.stackexchange.com/questions/3567590/a-directed-bichromatic-tournament.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n;
int arr[1005][1005];
int ans[1005][1005];
void solve(vector<int> v){
int mx=v[0];
for (auto it:v) if (arr[it][mx]) mx=it;
bool ok=true;
for (auto it:v) if (arr[it][mx]) ok=false;
if (ok){
for (auto a:v) for (auto b:v) if (arr[a][b]) ans[a][b]=2;
return;
}
vector<int> s,t;
int a=v[0];
rep(x,1,sz(v)){
if (arr[v[x]][a]){
ans[v[x]][a]=1;
s.pub(v[x]);
}
else{
ans[a][v[x]]=2;
t.pub(v[x]);
}
}
for (auto a:t) for (auto b:t) if (arr[a][b]) ans[a][b]=2;
for (auto a:s) for (auto b:t){
if (arr[a][b]) ans[a][b]=1;
if (arr[b][a]) ans[b][a]=3;
}
solve(s); //should not be empty
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n;
rep(x,1,n+1){
rep(y,1,n+1) cin>>arr[x][y];
int tot=0;
rep(y,1,n+1) tot+=arr[x][y];
if (tot==n-1){
cout<<"-1"<<endl;
return 0;
}
}
vector<int> v;
rep(x,1,n+1) v.pub(x);
solve(v);
cout<<3<<endl;
rep(x,1,n+1){
rep(y,1,n+1) cout<<ans[x][y]<<" "; cout<<endl;
}
}
I also found out that there is a much simpler solution, from Agnus, the problem author.
Instead of using vertex $1$ in the above construction, use the vertex $d$ with the greatest outdegree. Then, then following coloring scheme works.
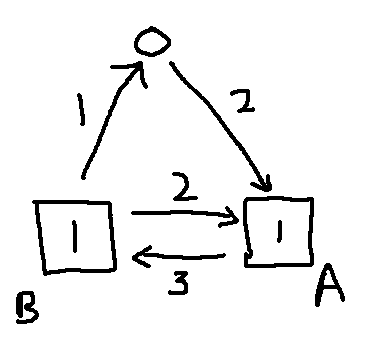
Again: It is clear that vertex $1$ and all vertices in $A$ satisfy the condition.
To prove that vertices in $B$ satisfy the condition, note that it is impossible for a vertex in $B$ to have an edge to all vertex in $A$ or else it will have a greater outdegree than vertex $d$.
We also colored the color scheme in that specific way so that a the below simple code works.
Code
#include <cstdio>
using namespace std;
const int N = 1050;
int col[2][2] = { {1, 2}, {3, 1} };
int n, deg[N], a[N][N];
int main() {
scanf("%d", &n);
int bst = 0;
for(int i = 0;i < n;i++) {
for(int j = 0;j < n;j++) {
scanf("%d", &a[i][j]);
deg[i] += a[i][j];
}
if(deg[i] > deg[bst]) bst = i;
}
if(deg[bst] == n - 1) {
printf("-1\n");
return 0;
}
printf("3\n");
for(int i = 0;i < n;i++) {
for(int j = 0;j < n;j++) {
printf("%d ", a[i][j] ? col[a[bst][i]][a[bst][j]] : 0);
}
printf("\n");
}
return 0;
}
Sirologija
Let us extend a definition of a hole to any cell that cannot be used on a path from $(1,1) \to (n,m)$. If we do a dfs from $(1,1)$ and from $(n,m)$, we can find which cells have a path $(1,1) \to (x,y)$ and $(x,y) \to (n,m)$.
Now, connect all the holes that are adjacent (both orthogonal and diagonally) with each other into groups. For two holes that are connected (directly or indirectly), that the minion can only go both above them or both below them.
Now, if there exists a path that goes from $(1,1) \to (n,m)$, then the answer is $1$ plus the number of groups that do not touch the boundary of the grid.
Code
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define ll long long
#define ii pair<int,int>
#define iii tuple<int,int,int>
#define fi first
#define se second
#define endl '\n'
#define debug(x) cout << #x << ": " << x << endl
#define pub push_back
#define pob pop_back
#define puf push_front
#define pof pop_front
#define lb lower_bound
#define ub upper_bound
#define rep(x,start,end) for(int x=(start)-((start)>(end));x!=(end)-((start)>(end));((start)<(end)?x++:x--))
#define all(x) (x).begin(),(x).end()
#define sz(x) (int)(x).size()
mt19937 rng(chrono::system_clock::now().time_since_epoch().count());
int n,m;
string grid[2005];
bool a[2005][2005];
bool b[2005][2005];
int p[2005*2005];
bool bad[2005*2005];
int par(int i){
if (p[i]==i) return i;
else return p[i]=par(p[i]);
}
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin.exceptions(ios::badbit | ios::failbit);
cin>>n>>m;
rep(x,0,n) cin>>grid[x];
a[0][0]=true;
rep(x,0,n) rep(y,0,m) if (grid[x][y]=='.'){
if (x && a[x-1][y]) a[x][y]=true;
if (y && a[x][y-1]) a[x][y]=true;
}
b[n-1][m-1]=true;
rep(x,n,0) rep(y,m,0) if (grid[x][y]=='.'){
if (x!=n-1 && b[x+1][y]) b[x][y]=true;
if (y!=m-1 && b[x][y+1]) b[x][y]=true;
}
rep(x,0,n) rep(y,0,m) a[x][y]&=b[x][y];
rep(x,0,n) rep(y,0,m) p[x*m+y]=x*m+y;
//rep(x,0,n){
//rep(y,0,m) cout<<a[x][y]; cout<<endl;
//}
rep(x,0,n) rep(y,0,m) if (!a[x][y]){
int z=par(x*m+y);
if (x && !a[x-1][y]){
int t=par((x-1)*m+y);
p[t]=z;
bad[z]|=bad[t];
}
if (y && !a[x][y-1]){
int t=par(x*m+(y-1));
p[t]=z;
bad[z]|=bad[t];
}
if (x && y && !a[x-1][y-1]){
int t=par((x-1)*m+(y-1));
p[t]=z;
bad[z]|=bad[t];
}
if (x==0 || x==n-1 || y==0 || y==m-1) bad[z]=true;
}
int ans=0;
rep(x,0,n) rep(y,0,m) if (!a[x][y] && par(x*m+y)==x*m+y && !bad[x*m+y]) ans++;
if (a[0][0]) ans++;
cout<<ans<<endl;
}