• $\frac{d}{dx} \sin(x) = \cos(x)$
  • $\frac{d}{dx} \cos(x) = - \sin(x)$
  • $\frac{d}{dx} \tan(x) = \sec^2(x)$
  • $\frac{d}{dx} \sec(x) = \sec(x) \tan(x)$
  • $\frac{d}{dx} \arcsin(x) = \frac{1}{\sqrt{1-x^2}}$
  • $\frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}$

Mean Value Theorem: Let $f$ a function that is continuous on $[a,b]$ and differentiable on $(a,b)$, then there exists $a<c<b$ such that $f’(c) = \frac{f(b)-f(a)}{b-a}$.

Intermediate Value Theorem: Let $f$ be a function that is continuous on $[a,b]$, then there exists a $a < c < b$ such that $f(c)=k$ where $k$ is any value between $f(a)$ and $f(b)$, excluding endpoints.

Rolle’s Theorem: Mean Value Theorem but $f(a)=f(b)$, so that $f’(c)=0$.

  • If $f’(x) \geq 0$ on $x \in [a,b]$, then $f$ is increasing on $x \in [a,b]$
  • If $f’(x) \leq 0$ on $x \in [a,b]$, then $f$ is decreasing on $x \in [a,b]$
  • If $f$ is increasing on $x \in (a,b)$, then $f$ is concave up on $x \in (a,b)$
  • If $f$ is decreasing on $x \in (a,b)$, then $f$ is concave down on $x \in (a,b)$

If $f’(c)=0$, then $x=c$ is a stationary point. There are 3 cases:

  • If $f^{\prime\prime}(x) > 0$, then $x=c$ is a relative minimum
  • If $f^{\prime\prime}(x)<0$, then $x=c$ is a relative maximum
  • Else if $f’(x) < 0$ for $(a,c)$ and $f’(x) > 0$ for $(c,b)$, then $x=c$ is a relative minimum
  • Else if $f’(x) > 0$ for $(a,c)$ and $f’(x) < 0$ for $(c,b)$, then $x=c$ is a relative maximum
  • Else, neither a relative minimum nor maximum

If $f^{\prime\prime}(c)$ changes sign, then it is known as an inflection point. You have to explicitly say that $f^{\prime\prime}(c)$ changes sign from positive to negative or vice versa.

$f^{\prime\prime}(x)<0$ means that $f$ is concave down and $f^{\prime\prime}(x)>0$ means that $f$ is concave up.

$\frac{d}{dx} \int_a^b f(t) \, dt = f(b)-f(a)$

Infinite series convergence tests:

  • check n-th term approaches $0$
  • limit comparison test
  • comparison test $a_i \leq b_i$
  • integral test
  • alternating series test, series has terms which alternate in sign, terms decrease in absolute value and approach $0$
  • ratio test, calculate $L = \lim \limits_{x \to \infty} \lvert \frac{a_{x+1}}{a_x} \rvert$

For an alternative series $\sum (-1)^i a_i$, the error bound for $\sum\limits_{i=0}^{n} (-1)^i a_i$ is at most $\lvert a_{n+1} \rvert$.

The Taylor series of a function is $f(x) = \sum\limits_{i=0}^\infty \frac{f(c)^{(i)}(x-c)^i}{i!}$. Usually, we take $c=0$.

Suppose that $g(x)$ is the approximation of $f(x)$ up to $x^k$, so the error of the Taylor approximation is $r(x) = f(x) - g(x)$. Taylor’s theorem states that $\lvert r(x) \rvert \leq \frac{M (x-c)^{k+1}}{(k+1)!}$, where $M$ is the maximum value of $\lvert f^{(k+1)}(x)\rvert$ on the interval between $c$ and $x$.

Some common Taylor series:

  • $\frac{1}{1+x} = 1 - x + x^2 - x^3 + x^4 - \ldots$
  • $\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \ldots$
  • $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots$
  • $\cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \frac{x^8}{8!} + \ldots$
  • $\sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \frac{x^9}{9!} + \ldots$

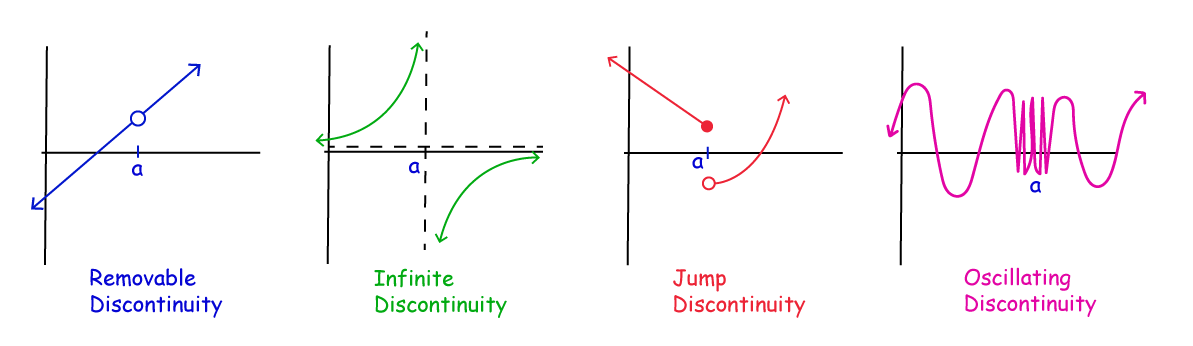
Note that infinite discontinuity can be referred to as essential discontinuity.

Logistic differential equation is given by $\frac{dP}{dt} = kP(1-\frac{P}{L})$.

<
Previous Post
Reading Fromkin’s Introduction to Language
>
Next Post
Japanese Grammar Notes 1