AP Physics C Mech Crib Notes
Kinematics
If we have functions $x(t),v(t),a(t)$ representing position, velocity and acceleration, then we have $v=\frac{d}{dt} x$ and $a=\frac{d^2}{dt^2} x$. Speed is defined as $ \lvert v(t) \rvert$, read question properly if asking for velocity or speed.
For forces, generally $F=ma$. For friction force, it is applied by a surface with coefficients of friction $\mu_s$ and $\mu_k$ respectively for static and kinetic, when the object is not moving and moving respectively. If the surface has normal force $N$ on the object, the static and kinetic frictions are $\mu_sN$ and $\mu_k N$ respectively.
For higher dimensions, just split into components using trigo. As $x(t),v(t),a(t)$ are all independent across dimensions.
Work, Power, Energy
The definition of work is $W = \int \vec F \, d \vec x$. Note that it is integrating over the cross product of $\vec F$ and $d \vec x$, so the direction matter. For usual 1D case with constant force, we have $W = F d$.
Power is defined as $P=\frac{d}{dt} W = \frac{\Delta W}{t}$. If we have constant force and velocity, $P = Fv$.
For now, we are only concerned with translational kinectic energy and gravitational potential energy.
$KE = \frac{1}{2} mv^2$ and $GPE = mgh$.
Then, we have $\Delta W = (KE_2+GE_2) - (KE_1+GE_1)$.
This has some unintuitive results, such that as long as a ball’s speed is unchanged, we can change its direction without any work. However, surely a bent pipe can change the ball’s direction without doing any work.
Momentum
Momentum is defined as $p = mv$. Impulse is defined as the change in momentum or $J = p_2 - p_1$.
For higher dimensions, momentum is independent across dimensions.
Rotation
Define the angular velocity as $\omega = \frac{v}{r}$. It is defined such that $x(t) = \sin(w t)$ tracks the $x$-position on a circle of radius $1$ centered at the origin with linear speed of edge being $v$. $\omega$ is defined for convinience to plug into trigo equations. The frequency and period of the oscillation is $f = \frac{\omega}{\tau}$ and $T = \frac{\tau}{\omega}$.
To maintain the circular path, the object has to be constantly accelerated towards the axis of the rotation with acceleration $a_{rad} = \frac{v^2}{r} = w^2 r$. The tangential acceleration is only responsible for increasing the speed of the object and it can be treated as 1D motion.
For angular momentum and energy, we define the moment of inertia $I = \sum_i m_i r_i^2 = \iiint_Q p(x,y,z) \lVert r \rVert^2 \, dV$. It is the analogue of mass for rational mechanics.
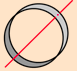
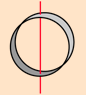
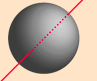
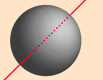
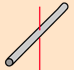
Some common values of $I$ are as follow:
| Hoop about symmetric axis | Hoop about diameter | Solid Sphere | Hollow Sphere | Rod about center | Rod about side |
|---|---|---|---|---|---|
 |
 |
 |
 |
 |
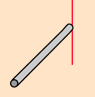 |
| $I=MR^2$ | $I=\frac{1}{2}MR^2$ | $I=\frac{2}{5}MR^2$ | $I=\frac{2}{3}MR^2$ | $I=\frac{1}{12}MR^2$ | $I=\frac{1}{3}MR^2$ |
| All mass is distance $R$ away. | $\int_{0}^\tau sin^2 \theta \, d \theta = \frac{\tau}{2}$ | $\int_{0}^{1} 2 \tau r^3 \sqrt{1-r^2} \, dr = \frac{4\tau}{15}$ | $\int_{0}^{\frac \tau 2} \tau sin^3 \theta \, d\theta = \frac{4\tau}{3}$ | $\int_{0}^{\frac 12} 2 x^2 \, dx = \frac{1}{12}$ | $\int_{0}^{1} x^2 \, dx = \frac{1}{3}$ |
We also have the parrallel axis theorem. Which states that $I = I_{\text{CM}} + md^2$ where the axis is displaced from the center of mass by distance $d$. This is because $I = \int \lVert \vec x + \vec d \rVert \, dm = \int \vec x \cdot \vec x \, dm + 2\int \vec x \cdot \vec y \, dm + \int \vec y \cdot \vec y \, dm = I_{\text{CM}} + 0 + md^2$. The second term is $0$ since $\int \vec x \, dm = \vec 0$ as the average of the vectors $\vec x$ must be the position of the center of mass, which is the origin.
The rotational angular momentum is defined as $L = I\omega$ and the rotational kinetic energy is defined as $KE_{rot} = \frac{1}{2} I \omega^2$.
Rolling without slipping is when a sphere rolls on a floor and the contact point has $0$ speed.
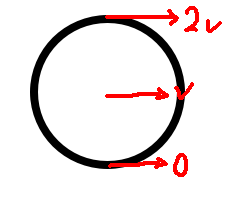
We have $\omega = \frac{v}{r}$. So $KE_{tot} = KE_{trans} + KE_{rot} = \frac{1}{2} mv^2 + \frac{1}{2} I\omega^2 = \frac{v^2}{2} (m + \frac{I}{r^2})$. A ball can roll without slipping on a frictionless surface if it has constant velocity. However, if it has changing velocity, it needs friction force to convert translational speed into rotational speed so that it can be maintain rolling without slipping
Simple Harmonic Motion
Simple harmonic motion (SHM) happens when the restoring force of a system is linear to its displacement. The two instances where this is studied are springs and pendulums. In springs, the restoring force is $kx$, while in a pendulum, the restoring force is $mg \sin \theta \approx mg \theta$. For pendulums, we will use the small angle approximation so that the system becomes SHM. The differential equation setup is $ma = m \ddot x = - kx$.
The ODE $a(t) = \frac{d^2}{dx^2} x(t)= - \omega^2 \cdot x(t)$ for some $c$ describes the SHM system. A solution to this ODE is $x(t) = b_1 \sin(\omega t + b_2)$. We find that $v(t) =\omega b_1 \cos(\omega t + c_2)$ and $a(t) = - \omega^2 b_1 \sin(\omega t + c_2) = - \omega^2 \cdot x(t)$.
Since the pair $(\cos \theta, \sin \theta)$ geometrically traces out the path of a constant velocity particle moving in a unit circle, it is convenient for us to think about this as circular motion. Therefore, we may define $\omega$ geometrically as the rotational speed of the SHM system (in radians per second) when projected onto a unit circle. We will also define the frequency and period as $f = \frac{w}{\tau}$ and $T = \frac{1}{f}$.
For a spring system, $a(t) = - \frac{F}{m} = - \frac{k x(t)}{m}$. Therefore, $\omega = \sqrt\frac{k}{m}$.
For a pendulum system, $a(\theta) = - \frac{F}{m} = - \frac{mg \theta}{m} = - g \theta= - g \frac{x(t)}{L}$. Therefore, $\omega = \sqrt \frac{g}{L}$.
Gravity
The force of gravity between two objects is $F = \frac{GMm}{r^2}$. Note that we define the gravitational constant of earth as $g = \frac{GM_{\text{earth}}}{r_{\text{earth}}^2}$.
Earlier, we defined an object to have GPE. But to be more precise, GPE is a quantity that exists between a system of two objects. As convention, we define the GPE of two objects infinitely far apart to be $0$. Then, then GPE of two objects is $\int_{\infty}^R \frac{GMm}{r^2} \, dr = -\frac{GMm}{r}$. It is fine that GPE is negative. This is because we only care about the relative change in energy. Indeed, for GPE defined earlier, we consider the GPE to be $0$ when we have $r = r_{\text{earth}}$, we also use the approximation $\frac{GMm}{r} - \frac{GMm}{r+h} = \frac{GMm h}{r(r+h)} \approx m \cdot \frac{GM}{r^2} \cdot h = mgh$ Indeed for translational KE, it is dependent on our frame of reference. If the observer moves, the KE will also change.
Circular Orbit
From circular motion, we know that $a = \frac{v^2}{r}$, therefore, $\frac{GMm}{r^2} = F = \frac{mv^2}{r}$, which simplifies into $GM=v^2r$.
Elliptical Orbit
Kepler’s Laws:
- Kepler’s First Law: The orbit forms an ellipse with one of the foci points is the sun
- Kepler’s Second Law: a line between the sun and the planet sweeps out an equal area over an equal time interval, proof by conservation of angular momentum
- Kepler’s Third Law: square of planet’s orbital period is proportional to cube of length of semi-major axis of orbit, proof can be guessed by solving for circular orbits
Conservation rules
Momentum is always conserved, it can be spammed for equations. Energy may not be conserved, never assumed that it is conserved. Note that the system must be closed for conservation rules to work. For example, a human pushing a ball does not violate COE as the human has stored potential energy to activate muscles. Another example is a ball bouncing on the ground. COM does not hold as we did not consider the change in momentum of the ground (the earth).
Note that for COAM, angular momentum is conserved around a single axis. For example, if you bring $2$ spinning disks together, the angular momentum about their respective axis will not add up. Instead you should choose a specific axis and consider the other’s AM about that axis using the full form of the angular moment formula $\vec L = \vec R \times m \vec v_{\text{CM}} + I_{\text{CM}} \vec \omega$. Note that for a ball moving in a straight line, COAM is also preserved, as $\lvert \vec L \rvert = \lvert \vec R \times m \vec v \rvert = m \lvert \vec R \rvert \lvert \vec v \rvert \sin \theta = m \lvert \vec v \rvert \lvert R_{\perp} \rvert$.