Trigonometry

Trigonometry

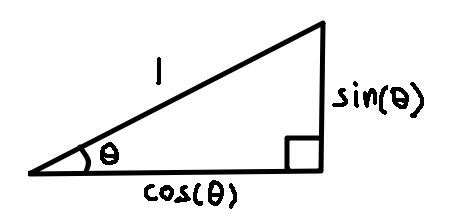
Define $\sin (\theta )$ and $\cos (\theta )$ as the side lengths of the above triangle. Note that these values are defined for all real values of $\theta$, for example with $\frac{\tau }{4}<\theta <\frac{\tau }{2}$, $\sin (\theta )$ is positive but $\cos (\theta )$ is negative.

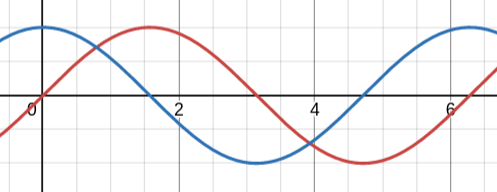
In the above graph, the red line is $\sin$ while the blue line is $\cos$.

Observe that $\sin (\theta )=\cos (\theta -\frac{\tau }{4})$ and $sin(\theta )=-\sin (\theta +\frac{\tau }{2})$. Since $\sin$ and $\cos$ are odd and even functions respectively, we have $\sin (\theta )=-\sin (-\theta )$ and $\cos (\theta )=\cos (-\theta )$. Since both functions are $\tau$-periodic, we also have $\sin (\theta )=\sin (\theta +\tau )$ and $\cos (\theta )=\cos (\theta +\tau )$.

By the Pythagorean theorem, we also have ${\sin }^2(\theta )+{\cos }^2(\theta )=1$. Note that ${\sin }^a(\theta )$ is shorthand for $(\sin (\theta ){)}^a$ for positive $a$. ${\sin }^{-1}(\theta )$ means something else entirely.

We also define the function $\tan (\theta )=\frac{\sin (\theta )}{\cos (\theta )}$. Intuitively, it is the gradient of the line with angle $\theta$. Below is the graph of $\tan$.

Along with those three functions, we also have $\csc (\theta )=\frac{1}{\sin (\theta )}$, $\sec (\theta )=\frac{1}{\cos (\theta )}$ and $\cot (\theta )=\frac{1}{\cot (\theta )}$. They exist for historical reasons because of function tables. We really only need $\sin$ and $\cos$.

Sine Rule

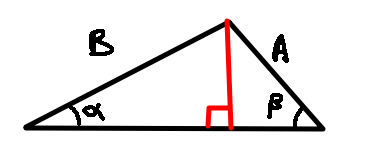
$\frac{\sin (\alpha )}{A}=\frac{\sin (b)}{B}$

Proof:
Drop the red perpendicular line. The length of the perpendicular line is $A\sin (\beta )$ or $B\sin (\alpha )$.
Since we have $A\sin (\beta )=B\sin (\alpha )$, $\frac{\sin (\alpha )}{A}=\frac{\sin (b)}{B}$ follows.

Addition of Trigonometric Functions

$\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )$

Proof:

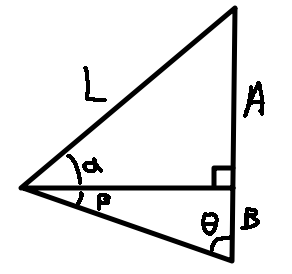
In the above diagram, we have $\frac{A+B}{\sin (\alpha +\beta )}=\frac{L}{\sin (\theta )}$ by sine rule and $A=L\sin (\alpha )$ by the definition of $\sin$.

$\frac{A+B}{\sin (\alpha +\beta )}=\frac{L}{\sin (\theta )}=\frac{A}{\sin (\alpha )\sin (\theta )}=\frac{A}{\sin (\alpha )\sin (\frac{\tau }{4}-\beta )}=\frac{A}{\sin (\alpha )\cos (\beta )}$

Therefore, $(A+B)\cdot (\sin (\alpha )\cos (\beta ))=A\cdot (\sin (\alpha +\beta ))$
By symmetry, we also have $(A+B)\cdot (\sin (\beta )\cos (\alpha ))=B\cdot (\sin (\alpha +\beta ))$
Adding both equations, we obtain $(A+B)\cdot (\sin (\alpha )\cos (\beta )+\sin (\beta )\cos (\alpha ))=(A+B)\cdot (\sin (\alpha +\beta ))$
Therefore, $\sin (\alpha +\beta )=\sin (\alpha )\cos (\beta )+\cos (\alpha )\sin (\beta )$

Corollary: $\sin (\alpha \pm \beta )=\sin (\alpha )\cos (\beta )\pm \cos (\alpha )\sin (\beta )$

Corollary: $\cos (\alpha \pm \beta )=\cos (\alpha )\cos (\beta )\mp \sin (\alpha )\sin (\beta )$
Proof: $\cos (\alpha \pm \beta )=\sin ((\alpha +\frac{\tau }{4})\pm \beta )=\sin (\alpha +\frac{\tau }{4})\cos (\beta )\pm \cos (\alpha +\frac{\tau }{4})\sin (\beta )=\cos (\alpha )\cos (\beta )\mp \sin (\alpha )\cos (\beta )$

Corollary: $\sin (2\theta )=2\sin (\theta )\cos (\theta )$ and $\cos (2\theta )={\cos }^2(\theta )-{\sin }^2(\theta )=2{\cos }^2(\theta )-1=1-{\sin }^2(\theta )$

Product to Sum

$2\sin (\alpha )\cos (\beta )=\sin (\alpha +\beta )+\sin (\alpha -\beta )$
$2\cos (\alpha )\sin (\beta )=\sin (\alpha +\beta )-\sin (\alpha -\beta )$
$2\cos (\alpha )\cos (\beta )=\cos (\alpha +\beta )+\cos (\alpha -\beta )$
$2\sin (\alpha )\sin (\beta )=-\cos (\alpha +\beta )+\cos (\alpha -\beta )$

Proofs: expand right side

Sum to Product

If we write $u=\alpha +\beta$ and $v=\alpha -\beta$ above, then $\alpha =\frac{u+v}{2}$ and $\beta =\frac{u-v}{2}$.

Inverse Trigonometric Functions

$\arcsin (\theta )$ is defined as the functional inverse of the function $\sin (\theta )$. However, $\sin$ is not injective as $\sin (0)=\sin (\frac{\tau }{2})=0$. Therefore, we restrict the domain of $\sin$ into $\sin :[-\frac{\tau }{4},\frac{\tau }{4}]\to [-1,1]$, so that we have $\arcsin :[-1,1]\to [-\frac{\tau }{4},\frac{\tau }{4}]$.

Similarly, we have $\arccos :[-1,1]\to [0,\frac{\tau }{2}]$ and $\arctan :\mathbb{R}\to [-\frac{\tau }{4},\frac{\tau }{4}]$.

The graphs in green, purple and red are respectively $\arcsin$, $\arccos$ and $\arctan$.

$\csc$, $\sec$ and $\cot$ also have their analogous inverse functions.

Note that most people write $\arcsin$ as ${\sin }^{-1}$.

Differentiation of Trigonometric Functions

By definition, $\frac{d}{dx}f(x)=\underset{h\to 0}{lim}\frac{f(x+h)-f(x)}{h}$

$\frac{d}{dx}\sin (x)=\underset{h\to 0}{lim}\frac{\sin (x+h)-\sin (x)}{h}=\underset{h\to 0}{lim}\frac{\sin (x)\cos (h)+\cos (x)\sin (h)-\sin (x)}{h}$

Since $\underset{h\to 0}{lim}\cos (h)=1$, we have $\frac{d}{dx}\sin (x)=\underset{h\to 0}{lim}\frac{\sin (x)\cos (h)+\cos (x)\sin (h)-\sin (x)}{h}=\underset{h\to 0}{lim}\frac{\sin (x)(1)+\cos (x)\sin (h)-\sin (x)}{h}=\cos (x)\underset{h\to 0}{lim}\frac{\sin (h)}{h}$

Now, we will need to find $\underset{h\to 0}{lim}\frac{\sin (h)}{h}$.

In the above diagram, the area of triangle $ABC$, sector $ABC$ and triangle $ABD$ are $\frac{1}{2}\sin (x)$, $\frac{1}{2}x$ and $\frac{1}{2}\tan (x)$ respectively.

So for positive small $x$, we have $\sin (x)<x<\tan (x)$. Dividing all sides by $\sin x$, we obtain $1<\frac{x}{\sin (x)}<\frac{1}{\cos (x)}$.

Since $\underset{x\to 0^{+}}{lim}1=1$ and $\underset{x\to 0^{+}}{lim}\frac{1}{\cos (x)}=1$, we have $\underset{x\to 0^{+}}{lim}\frac{x}{\sin (x)}=1$.

Since $\sin$ is an odd function, $\underset{x\to 0^{-}}{lim}\frac{x}{\sin (x)}=\underset{x\to 0^{+}}{lim}\frac{-x}{\sin (-x)}=\underset{x\to 0^{-}}{lim}\frac{-x}{-\sin (x)}=\underset{x\to 0^{-}}{lim}\frac{x}{\sin (x)}=1$.

Therefore, $\frac{d}{dx}\sin (x)=\cos (x)\underset{h\to 0}{lim}\frac{\sin (h)}{h}=\cos (x)$.

Corollary: $\frac{d}{dx}\cos (x)=\frac{d}{dx}\sin (x+\frac{\tau }{4})=\cos (x+\frac{\tau }{4})=\sin (x+\frac{\tau }{2})=-\sin (x)$.

The derivative of the other trigonometric functions are easy to derive using derivative rules. In summary:

• $\frac{d}{dx}\sin (x)=\cos (x)$
• $\frac{d}{dx}\cos (x)=-\sin (x)$
• $\frac{d}{dx}\tan (x)={\sec }^2(x)$
• $\frac{d}{dx}\csc (x)=-\csc (x)\cot (x)$
• $\frac{d}{dx}\sec (x)=\sec (x)\tan (x)$
• $\frac{d}{dx}\cot (x)=-{\csc }^2(x)$

Since we have the derivatives of $\sin$ and $\cos$, we can write out its Taylor expansion.

$\sin (x)=\frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\dots$

$\cos (x)=\frac{1}{0!}-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\dots$

Their Taylor expansion is very closely related to the Taylor expansion of $e^x$. Indeed, it is the “simplest” functions that satisfy the differential equation $\frac{d^2}{d^{2}x}f(x)=-f(x)$.

Consider the function $e^{ix}$ which traces out a circle with radius $1$. We have $e^{ix}=\cos (x)+i\sin (x)$. Since we have $\frac{d^2}{d^x}{e}^{ix}=-e^{ix}=-\cos (x)-i\sin (x)$, it should be clear why $\sin$ and $\cos$ should satisfy the differential equation $\frac{d^2}{d^{2}x}f(x)=-f(x)$.

Note that using $e^{ix}=\cos (x)+i\sin (x)$ we can derive the formulas for addition of trigonometric functions.
$\cos (a+b)+i\sin (a+b)=e^{i(a+b)}=e^{ia}\cdot e^{ib}=(\cos (a)+i\sin (a))\cdot (\cos (b)+i\sin (b))=(\cos (a)\cos (b)-\sin (a)\sin (b))+i(\sin (a)\cos (b)+\cos (a)\sin (b))$

Differentiation of Inverse Trigonometric Functions

$1=\frac{d}{dx}x=\frac{d}{dx}f(f^{-1}(x))=f^{\prime }(f^{-1}(x))\cdot \frac{d}{dx}{f}^{-1}(x)$

Therefore, $\frac{d}{dx}{f}^{-1}(x)=\frac{1}{f^{\prime }(f^{-1}(x))}$.

So, we have $\frac{d}{dx}\arcsin (x)=\frac{1}{\cos (\arcsin (x))}$.

In the above diagram, $\cos (\arcsin (x))=\cos (\theta )=\sqrt{1-x^2}$

Therefore, $\frac{d}{dx}\arcsin (x)=\frac{1}{\sqrt{1-x^2}}$.

Similarly, $\frac{d}{dx}\arccos (x)=\frac{1}{-\sin (\arccos (x))}=-\frac{1}{\sqrt{1-x^2}}$

$\frac{d}{dx}\arctan (x)={\cos }^2(\arctan (x))$

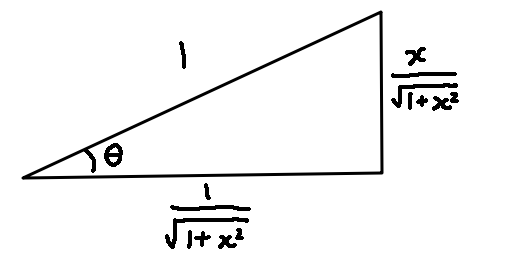
In the above diagram, ${\cos }^2(\arctan (x))={\cos }^2(\theta )=\frac{1}{1+x^2}$

Therefore, $\frac{d}{dx}\arctan (x)=\frac{1}{1+x^2}$

Hyperbolic Functions

The hyperbolic functions are the analogue of the trigonometric functions. While the trigonometric functions satisfy ${\cos }^2+{\sin }^2=1$ and $\frac{d^2}{d^{2}x}f(x)=-f(x)$, the hyperbolic functions satisfy ${\cosh }^2-{\sinh }^2=1$ and $\frac{d^2}{d^{2}x}f(x)=f(x)$. They are called hyperbolic functions because $x^2-y^2=1$ is the graph of the unit hyperbola. Apparently they appear as solutions to Laplace equations.

The definition of $\sinh$ and $\cosh$ are $\sinh (x)=\frac{e^x-e^{-x}}{2}$ and $\cosh (x)=\frac{e^x+e^{-x}}{2}$. This is similar to the definitions of $i\cdot \sin (x)=\frac{e^{ix}-e^{-ix}}{2}$ and $\cos (x)=\frac{e^{ix}+e^{-ix}}{2}$.

We can verify that ${\cosh }^2(x)-{\sinh }^2(x)=(\frac{e^x+e^{-x}}{2}{)}^2-(\frac{e^x-e^{-x}}{2}{)}^2=\frac{(e^{2x}+2+e^{-2x})-(e^{2x}-2-e^{-2x})}{4}=1$.

Addition of Hyperbolic Functions

$\sinh (x\pm y)=\sinh (x)\cosh (y)\pm \cosh (x)\sinh (y)$
$\cosh (x\pm y)=\cosh (x)\cosh (y)\pm \sinh (x)\sinh (y)$

They should be similar to the normal trigonometric function if one inspects how they are written in terms of $e^x$ or $e^{ix}$ respectively. The only difference are in the signs.

Corollary: $\sinh (2x)=2\sinh (x)\cosh (x)$ and $\cosh (2x)={\cosh }^2(x)+{\sinh }^2(x)=2{\cosh }^2(x)-1=1+2{\sinh }^2(x)$

Inverse Hyperbolic Functions

Define $\text{arcsinh}:\mathbb{R}\to \mathbb{R}$, $\text{arcsinh}:[1,\mathrm{\infty })\to [0,\mathrm{\infty })$ and $\text{arctanh}:[-1,1]\to \mathbb{R}$ as the functional inverses of $\sinh$, $\cosh$ and $\tanh$ respectively.

We can find explicit formulas for these three functions.

Let $y=\text{arcsinh}(x)$, then $\sinh (y)=x$
$e^y=\sinh (y)+\cosh (y)=\sinh (y)+\sqrt{1+{\sinh }^2(y)}=x+\sqrt{1+x^2}$
$\text{arcsinh}(x)=\ln (x+\sqrt{1+x^2})$

Let $y=\text{arccosh}(x)$, then $\cosh (y)=x$
$e^y=\sinh (y)+\cosh (y)=\sqrt{{\cosh }^2(y)-1}+\cosh (y)=\sqrt{x^2-1}+x$
$\text{arcsinh}(x)=\ln (x+\sqrt{x^2-1})$

Let $y=\text{arctanh}(x)$, then $\tanh (y)=x$
$1-\tanh (y)=1-\frac{e^y-e^{-y}}{e^y+e^{-y}}=\frac{-2e^{-y}}{e^y+e^{-y}}=\frac{2}{e^{2y}+1}$
$e^{2y}=\frac{2}{1-x}-1=\frac{1+x}{1-x}$
$\text{arctanh}(x)=\frac{1}{2}\ln (\frac{1+x}{1-x})$

Differentiation of Hyperbolic Functions

$\frac{d}{dx}\sinh (x)=\frac{d}{dx}\frac{e^x-e^{-x}}{2}=\frac{e^x+e^{-x}}{2}=\cosh (x)$
$\frac{d}{dx}\cosh (x)=\frac{d}{dx}\frac{e^x+e^{-x}}{2}=\frac{e^x-e^{-x}}{2}=\sinh (x)$
$\frac{d}{dx}\tanh (x)=\frac{d}{dx}\frac{\sinh (x)}{\cosh (x)}=\frac{{\cosh }^2(x)-{\sinh }^2(x)}{{\cosh }^2(x)}=\frac{1}{{\cosh }^2(x)}$

$\frac{d}{dx}\text{arcsinh}(x)=\frac{1}{{\sinh }^{\prime }(\text{arcsinh(x)})}=\frac{1}{\cosh (\text{arcsinh(x)})}=\frac{1}{\sqrt{x^2+1}}$, since $\cosh (\theta )=\sqrt{{\sinh }^2(\theta )+1}$
$\frac{d}{dx}\text{arccosh}(x)=\frac{1}{{\cosh }^{\prime }(\text{arccosh(x)})}=\frac{1}{\sinh (\text{arccosh(x)})}=\frac{1}{\sqrt{x^2-1}}$, since $\sinh (\theta )=\sqrt{{\cosh }^2(\theta )-1}$
$\frac{d}{dx}\text{arctanh}(x)=\frac{1}{{\tanh }^{\prime }(\text{arctanh(x)})}={\cosh }^2(\text{arctanh(x)})=\frac{1}{1-x^2}$, since $\cosh (\theta )=\frac{1}{\sqrt{1-{\tanh }^2(\theta )}}$

Universal Trigonometric Substitution

Also known as Weierstrass substitution.

If we are integrating a function $f(\theta )$ that can be written in terms of $\sin (\theta )$ and $\cos (\theta )$, we can just apply the substitution $t=\tan (\frac{\theta }{2})$.

$\frac{d\theta }{dt}=\frac{d}{dt}2\arctan (t)=\frac{2}{1+t^2}$
$\sin (\theta )=2\sin (\frac{\theta }{2})\cos (\frac{\theta }{2})=\frac{2\frac{\sin (\frac{\theta }{2})}{\cos (\frac{\theta }{2})}\frac{\cos (\frac{\theta }{2})}{\cos (\frac{\theta }{2})}}{\frac{{\cos }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}+\frac{{\sin }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}}=\frac{2t}{1+t^2}$

$\cos (\theta )={\cos }^2(\frac{\theta }{2})-{\sin }^2(\frac{\theta }{2})=\frac{\frac{{\cos }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}-\frac{{\sin }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}}{\frac{{\cos }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}+\frac{{\sin }^2(\frac{\theta }{2})}{{\cos }^2(\frac{\theta }{2})}}=\frac{1-t^2}{1+t^2}$

$$\begin{array}{rl}\int \frac{1}{5+4\cos \theta }d\theta & =\int \frac{\frac{2}{1+t^2}}{5+4(\frac{1-t^2}{1+t^2})}dt,t=\tan (\frac{\theta }{2})\\ & =\int \frac{2}{5(1+t^2)+4(1-t^2)}dt\\ & =\int \frac{2}{9+t^2}dt\\ & =\frac{2}{3}\arctan (\frac{t}{3})\\ & =\frac{2}{3}\arctan (\frac{\tan (\frac{\theta }{2})}{3})\end{array}$$ $$\begin{array}{rl}\int {\sec }^6(\theta )d\theta & =\int \frac{1}{({\cos }^2(\theta ){)}^3}d\theta \\ & =\int \frac{1}{(\frac{\cos (2\theta )+1}{2}{)}^3}d\theta \\ & =\int \frac{\frac{1}{1+t^2}}{(\frac{1}{1+t^2}{)}^3}dt,t=\tan (\theta )\\ & =\int 1+2t^2+t^{4}dt\\ & =t+\frac{2}{3}{t}^3+\frac{1}{5}{t}^5\\ & =\tan (\theta )+\frac{2}{3}{\tan }^3(\theta )+\frac{1}{5}{\tan }^5(\theta )\end{array}$$ $$\begin{array}{rl}\int \sec (3\theta )\sec (\theta )d\theta & =\int \frac{2}{\cos (3\theta +\theta )+\cos (3\theta -\theta )}d\theta \\ & =\int \frac{2}{\cos (4\theta )+\cos (2\theta )}d\theta \\ & =\int \frac{2}{1+\cos (2\theta )-2{\sin }^2(2\theta )}d\theta \\ & =\int \frac{\frac{2}{1+t^2}}{(\frac{2}{1+t^2})-2(\frac{2t}{1+t^2}{)}^2}dt,t=\tan (\theta )\\ & =\int \frac{1+t^2}{1-3t^2}dt\\ & =\int -\frac{1}{3}+\frac{4}{3}\cdot \frac{1}{1-3t^2}dt\\ & =-\frac{1}{3}t+\frac{2}{3\sqrt{3}}\cdot \ln |\frac{\sqrt{3}+3t}{\sqrt{3}-3t}|\\ & =-\frac{1}{3}\tan \theta +\frac{2}{3\sqrt{3}}\cdot \ln |\frac{\sqrt{3}+3\tan \theta }{\sqrt{3}-3\tan \theta }|\end{array}$$

---

<

Previous Post

Some Greedy Problems

>

Next Post

High Dimensional Prefix Sums